- Distributed Storage System Basic Serie 2 - Amplification and RUM.
- Here is the concept of Amplification and RUM in storage system.
- The content is based on the Read, write & space amplification - pick 2, The RUM Conjecture and CRUM conjecture.I will present my understanding.
- Only summary, not details.
Read, write & space amplification - pick 2
- Good things come in threes, then reality bites and you must choose at most two. This choice is well known in distributed systems with CAP, PACELC and FIT. There is a similar choice for database engines. An algorithm can optimize for at most two from read, write and space amplification. This means one algorithm is unlikely to be better than another at all three.
- Such as B-tree has less read amplification, LSM-tree has less write amplification.
- Build a framework to describe the storage system. Read, write & space amplification.
- CAP: Consistency, Availability, Partition
(Dsitributed System)- PACELC: one has to choose between availability (A) and consistency (C) (as per the CAP theorem), but else (E), even when the system is running normally in the absence of partitions, one has to choose between latency (L) and consistency (C).
(Dsitributed System)- FIT: A three-way tradeoff between fairness, isolation, and throughput (FIT)
(Scalable database system which supports atomic distributed transactions)
Purpose
- Read, write and space amplification explain performance and efficiency when evaluating algorithms for real and potential workloads. They aren't a replacement for Big O notation. They usually assume a specific workload and configuration including RAM size, database size and type of storage.
- For database system, the amplification is more important than other evaluationg algorithms, since the system contains a lot of software and hardware components. And the test benachmark is also complicated.
Read Amp
- Read-amp is the amount of work done per logical read operation. This can be defined for in-memory databases, persistent databases assuming no cache (worst-case behavior) and persistent databases assuming some cache (average-case behavior).
- The work done in-memory can be the number of key comparisons and traditional algorithm analysis can be used.
- The work done on-disk includes the number of bytes transferred and seeks (seeks matter on disks, not on NVM).
- The work done can also include the cost of decompressing data read from storage which is a function of the read block size and compression algorithm.
- Read-amp is defined separately for point and range queries. For range queries the range length matters (the number of rows to be fetched). In Linkbench the average range query fetches about 20 rows.
- Read-amp can also be defined for point queries on keys that don't exist. Some algorithms use a bloom filter to avoid disk IO for keys that don't exist. Queries for non-existent keys is common in some workloads. Bloom filters can't be used for a range query. The most frequent query in Linkbench is a range query that includes an equality predicate on the first two columns of the range query index. With RocksDB we define a prefix bloom filter to benefit from that.
Write Amp
- Write-amp is the amount of work done per write operation. This can include the number of bytes written to storage and disk seeks per logical write operation. This can be split into in-memory and on-disk write-amp but I frequently ignore in-memory write-amp.
- There is usually a cost to pay in storage reads and writes following a logical write. With write-amp we are ignoring the read cost. The read cost is immediate for an update-in-place algorithm like a B-Tree as a page must be read to modify it. The read cost is deferred for a write-optimized algorithm like an LSM as compaction is done in the background and decoupled from the logical write. There is usually some write cost that is not deferred - updating in-memory structures and writing a redo log.
- With flash storage there is usually additional write-amp from the garbage collection done by the FTL to provide flash blocks that can be rewritten. Be careful about assuming too much about the benefit of sequential and large writes from a write-optimized database engine. While the physical erase block size on a NAND chip is not huge, many storage devices have something that spans physical erase blocks when doing GC that I will call a logical erase block. When data with different lifetimes ends up in the same logical erase block then the long-lived data will be copied out and increase flash GC write-amp (WAF greater than 1). I look forward to the arrival of multi-stream to reduce flash GC WAF.
Space Amp
- Space-amp is the ratio of the size of the database to the size of the data in the database. Compression decreases space-amp. It is increased by fragmentation with a B-Tree and old versions of rows with an LSM. A low value for space-amp is more important with flash storage than disk because of the price per GB for storage capacity.
The RUM Conjecture
The ubiquitous fight between the Read, the Update, and the Memory overhead of access methods for modern data systems
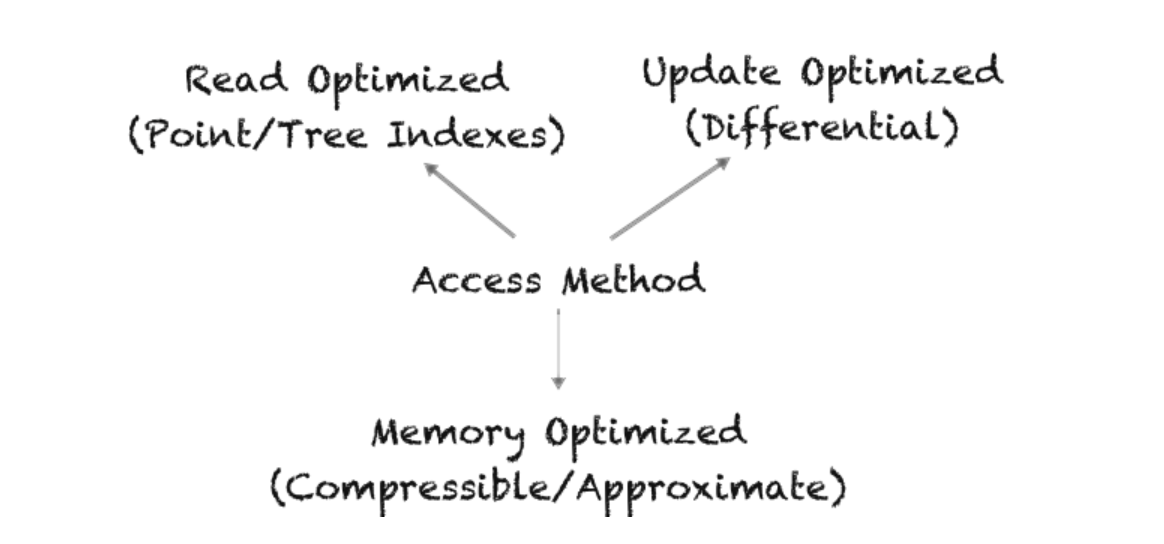
- The fundamental challenges that every researcher, systems architect, or developer faces when designing a new access method are how to minimize,
- i) read times (R),
- ii) update cost (U),
- iii) memory (or storage) overhead (M).
- In this project we first conjecture that when optimizing the read-update-memory overheads, optimizing in any two areas negatively impacts the third. Based on the RUM Conjecture, at DASlab, we study the manifestation of the balance of the RUM overheads in state-of-the-art access methods, and we pursue a path toward RUM-aware access methods for future data systems.
Rum Space
- When building access methods of modern systems, one is confronted with the same fundamental challenges, and design decisions. In particular, there are three quantities that researchers always try to minimize:
- (1) the read overhead (R),
- (2) the update overhead (U),
- (3) the memory (or storage) overhead (M)
- Deciding which overhead(s) to optimize for and to what extent, remains a prominent part of the process of designing a new access method, especially as hardware and workloads change over time.
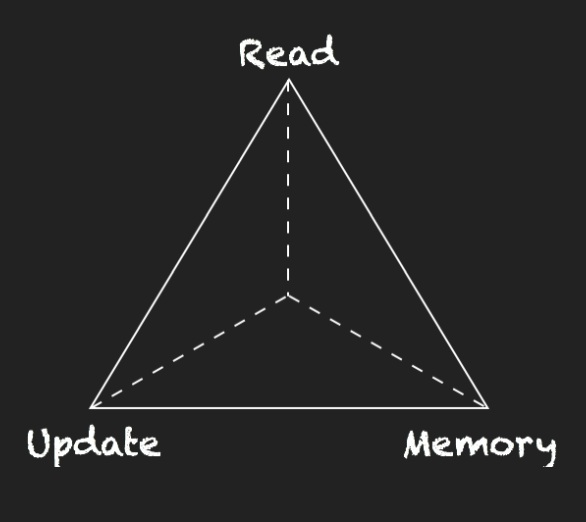
- The design space of the three RUM overheads can be seen as a three dimensional space or, if projected on a two-dimensional plane, as the triangle shown in the left hand-side, where each access method is mapped to a point or -- if it can be tuned to have varying RUM behavior -- to an area.
- Notice: This is a triangle, not a triangular pyramid. And the center of this triangle is Incentre.
Rum Conjecture
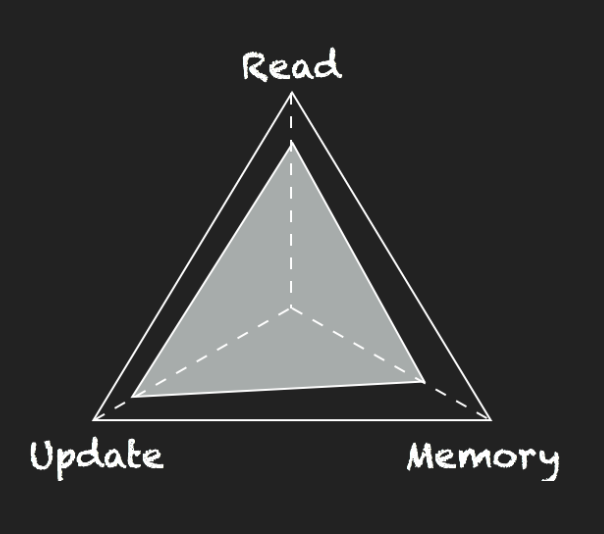
- An ideal solution is an access method that always provides the lowest read cost, the lowest update cost, and requires no extra memory or storage space over the base data.
- In practice, data structures are designed to compromise between the three RUM overheads, while the optimal design depends on a multitude of factors such as hardware, workload, and user expectations.
- Rum Conjecture: When designing access methods we set an upper bound for two of the RUM overheads, this implies a hard lower bound for the third overhead which cannot be further reduced.
Rum Overheads in Access Methods
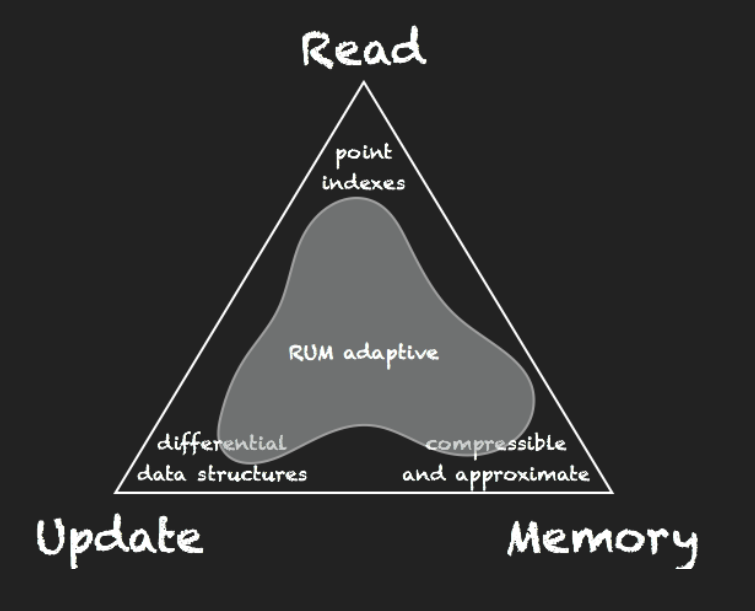
- Today, when building access methods, there is a wealth of approaches tailored for specific use cases.
- For example, in order to minimize the cost of updating data, one can use a design based on differential structures, allowing many queries to consolidate updates and avoid the cost of reorganizing data. Such an approach, however, increases the space overhead and hinders read cost as now queries need to merge any relevant pending updates during processing.
- Another example is that the read cost can be minimized by storing data in multiple different physical layouts, each layout being appropriate for minimizing the read cost for a particular workload. Update and space costs, however, increase because now there are multiple data copies. We further study how existing access methods balance the RUM overheads.
Toward Rum-Aware Access Methods
- The RUM Conjecture opens the path for exciting research challenges towards the goal of creating RUM-adaptive access methods. Future data systems should include versatile tools to interact with the data the way the workload, the application, and the hardware need and not vice versa. In other words, the application, the workload, and the hardware should dictate how we access our data, and not the constraints of our systems.
- Tuning access methods becomes increasingly important if, on top of big data and hardware, we consider the development of specialized systems and tools to cater data, aiming at servicing a narrow set of applications each. As more systems are built, the complexity of finding the right access method increases as well. As part of this project we design access methods with dynamic and tunable RUM behavior.
CRUM conjecture - read, write, space and cache amplification
- The C in CRUM is the amount of memory per key-value pair (or row) the DBMS needs so that either a point query or the first row from a range query can be retrieved with at most X storage reads. The C can also be reported as the minimal database : memory ratio to achieve at most X storage reads per point query.
Cache Amplification
- The cache-amp describes memory efficiency. It represents the minimal database : memory ratio such that a point query requires at most X storage reads. A DBMS with cache-amp=10 (C=10) needs 10 times more memory than one with C=100 to satisfy the at most X reads constraint.
- It can be more complicated to consider cache-amp for range seek and range next because processing them is more complicated for an LSM or index+log algorithm. Therefore I usually limit this to point queries.
- For a few years I limited this to X=1 (at most 1 storage read). But it will be interesting to consider X=2 or 3. With X=1:
- For a b-tree all but the leaf level must be in cache
- For an LSM the cache must include all bloom filter and index blocks, all data blocks but the max level
- For an index+log approach it depends (wait for another blog post)
