- VLDBJ 2018:LSM-based storage techniques: a survey
- 偶然的机会遇到一篇综述类型的文章,在考虑深入 LSM 的研究之前决定先阅读此篇
- 主要内容为 LSM 树的问题剖析相关方案的总结。
- ...
Abstract
- 近年来 LSM 树随着 NoSQL 的流行逐渐成为了数据库领域和操作系统领域的研究重点之一,旨在各方面对 LSM 树进行优化。这篇文章主要调研了 LSM 树的一些最新研究成果,便于读者了解 LSM 的发展动向。并使用了传统的分类方法对这些方案进行了分类,总结了优缺点。同时也提供了几个比较代表性的方案来探讨未来的发展方向。
- 关键字:LSM-tree,NoSQL,Storage Management,Indexing
Introduction
- LSM 树被广泛应用于现代的 NoSQL 存储系统中,如 BigTable,Dynamo,HBase,Cassandra,LevelDB,RocksDB and AsterixDB。LSM Tree 与传统的就地更新的索引结构有所不同,首先缓存将所有的写操作缓存在内存中,到达一定的阈值之后顺序地进行刷回到磁盘并进行合并。主要的优点则是较好的写性能,空间利用率高,具有可调性,并发控制和故障恢复机制较简单。所以 LSM Tree 能够为各种负载提供服务,典型代表 RocksDB 就被用于实时数据处理,图处理,流处理和联机事务处理(OLTP)。
- 由于 LSM 在现代存储系统中的流行,学术界提供了很多关于 LSM Tree的优化方案。本篇论文主要调查了近年来关于 LSM Tree 的相关研究,旨在为LSM研究者们提供一个指南。我们主要针对各个方案对于 LSM Tree的优化方案进行了分类,然后详细介绍各种改进,并讨论其优缺点。同时为了反映 LSM Tree的实际应用情况,我们也调查了五种开源的LSM Tree的NoSQL实现方案。
LSM Tree 基础
LSM Tree 发展历史
索引结构的更新策略
索引结构一般有两种更新策略。就地更新(in-place updates)和异地更新(out-of-place updates)。
.jpg)
- 就地更新 in-place updates:就地更新的典型代表为 B+树,直接将新数据写入覆盖老数据,因为确保了每次读的时候结果都是最新的,所以是读性能相对较好的,但牺牲了写性能,因为更新操作可能导致随机 IO,随机 IO 的性能一般比顺序 IO 差,除此以外,索引页可能因为删除和更新操作产生大量碎片,使得空间利用率降低。
- 优点:读性能较好
- 缺点:写性能较差,空间利用率低
- 异地更新 out-of updates:对比之下,LSM Tree 这种异地更新的方案,通常都是存储新的数据到新的位置,而不是直接覆盖老旧的数据。这种方案对应地就实现了 IO 的顺序写入,从而提升了写性能。由于没有覆盖老数据,数据恢复流程也得到了简化。但存在的最大问题就是牺牲了读性能,因为数据可能被存储在很多层,这样的结构就要求需要一套单独的数据重排机制来进行提升存储和查询的性能。
- 优点:写性能较好,数据恢复流程简单
- 缺点:读性能较差
异地更新/顺序写 思想起源
- 保证顺序写的异地更新思想早在上世纪七十年代就已经被应用到数据库系统中了,1976 年提出来的 Differential Files[1],就是将所有的更新首先写入到不同的文件中,然后由主文件周期地对其他文件进行合并。
- 80年代提出来的 Postgres[2] 则提倡使用日志结构化的数据库存储,通过将所有的写追加写入到顺序的日志文件中,从而支持快速的恢复和基于时间的查询,然后使用一个后台进程持续地对日志文件中的垃圾数据进行回收。该思想对应地后来被应用到文件系统领域,从而充分利用磁盘的写入带宽,例如日志结构化文件系统(LFS)[3]。
日志结构化存储的历史问题
在提出 LSM Tree 之前,日志结构化存储受限于几个关键问题,
- 数据存储在追加写的日志文件中导致的较低的查询性能。因为许多相关的数据是分散在日志文件中的;
- 老旧的数据没有被及时删除导致空间利用率不高。尽管设计了很多种数据重组方案,但是仍然缺少一个条理化的模型来分析写成本、读成本和空间利用率之间的权衡,这使得早期的日志结构存储很难进行参数调优。数据重新布局之后就很容易导致系统产生瓶颈。
LSM 的提出
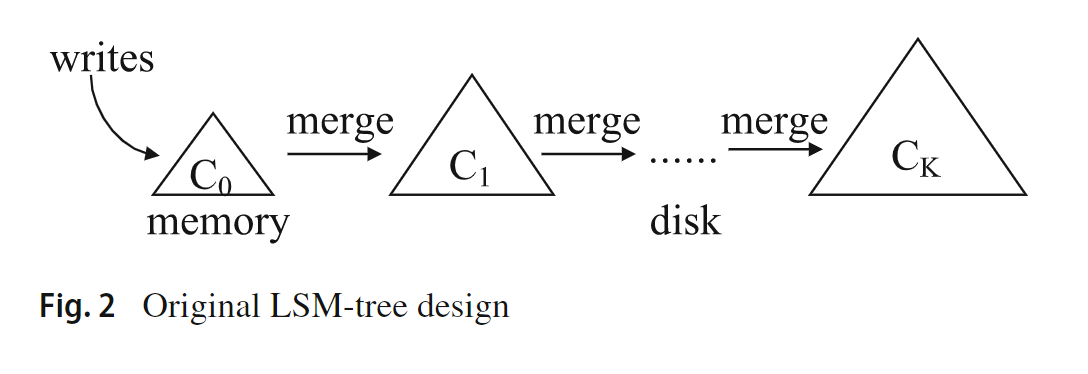
- 1996 年提出的 LSM Tree [4]则巧妙地解决了上述存在的问题。其中多层结构主要是借鉴 B+ 树,每一个层级都使用了 B+ 树的结构,并提出水平合并的策略 leveling merge policy [5] [6] 来进行数据压缩。最初提出的滚动合并过程由于其实现的复杂性而没有被今天的基于 LSM 的存储系统所使用。LSM 树的原始论文进一步表明,在稳定的工作负载下,当所有相邻组件之间的大小比 Ti = |Ci+1|/|Ci| 相同时,且层数保持不变的情况下,写性能得到了优化。这个原则影响了 LSM 树的所有后续实现和改进。
- 为了提升 LSM Tree 的并行性,Jagadish 等人提出了类似的结构和逐步合并策略,以获得更好的写性能。它将组件组织成一个 Level,当Level L 充满了 T 组件时,这些 T 组件将合并到 Level L+1 的新组件中。这个策略变成了现在的 LSM-tree 实现中使用的分层合并策略 tiering merge policy [5] [6]。
如今的 LSM Tree
基础结构
- 如今的 LSM Tree 仍然使用异地更新的策略来减少随机 IO,所有的写操作都首先追加写入到内存组件中,插入和更新操作都是直接写入一个新的键值对,而删除操作则是写入一个标记对来标志一个 Key 对应的 Entry 已经被删除了。然而如今的 LSM Tree 在实现过程中利用了磁盘组件的不变性来简化并发控制和恢复过程。多个磁盘组件被合并到一个新的磁盘组件中,而不用修改已经存在的组件。(区别于原论文提出的滚动合并机制)
- 针对 LSM Tree 的内部具体实现,内存组件常常使用并发的数据结构来实现,如跳表或者 B+ 树来组织他们的内存组件,磁盘组件一般使用 B+ 树或排序字符串表 SSTables 来组织。一个 SSTable 包含一个数据块列表和一个索引块; 数据块存储按键排序的键值对,索引块存储所有数据块对应的键范围。
- 对于 LSM-tree 的查询必须搜索多个组件来执行协调,即查找每个键对应的值的最新版本。获取特定键值的点查询可以逐个地从新到旧地搜索所有组件,并在找到第一个匹配项后立即停止。范围查询可以同时搜索所有组件,将搜索结果放入优先级队列中执行协调。
- 随着时间的推移,磁盘组件越来越多,LSM-tree 的查询性能会下降,因为查询时必须扫描更多的组件。为了解决这个问题,将逐步合并磁盘组件以减少组件的总数。通常有两种合并策略,都将磁盘组件组织成逻辑级别(或层),并由大小比例 T 控制。两种策略分别为 Leveling Merge Policy 和 Tiering Merge Policy
- Leveling Merge Policy 每一层只保留一个组件,但层级之间的大小比例仍保持为T,因此,组件在 Level L 将多次与 Level L-1 的传入组件合并,直到它被填满,然后它将被合并到 Level L+1。如图所示,L0 和 L1 合并以后将使得 L1 变得更大,因为每一层只保留一个组件。
- Tiering Merge Policy,该种合并策略每一层则维护了 T 个组件,当一层满了之后,对应的 T 个组件将合并成一个新的位于 L+1 层的组件,在图中,Level 0 的两个组件合并在一起,形成 Level 1 的新组件。应该注意的是,如果 Level L 已经是配置的最高级别,那么结果仍然位于Level L。
- 通常情况下,leveling merge policy 的查询性能更好,因为查询时需要检索的组件数更少,而 tiering merge policy 的写性能更好,因为减小了合并的频率。

Leveling Merge Policies
- 典型应用 RocksDB.
- 具体过程可以参考 RocksDB 的合并实现 Leveled Compaction:https://github.com/facebook/rocksdb/wiki/Leveled-Compaction
Tiering Merge Policy
- 典型应用 Cassendra
- 具体过程可以参考 https://www.scylladb.com/2018/01/17/compaction-series-space-amplification/
参考资料
一些其他方面的优化方案
- 有两种在绝大多数 LSM 存储中都使用到的优化方案:BloomFilter 和 Partitioning。
BloomFilter
- 一种节省空间的概率数据结构,用于响应集合成员查询。针对该数据结构的介绍请参考其他资料,此处不再赘述。
- 布隆过滤器主要是两个操作,一个是插入一个Key,一个是检查一个键的成员关系(是否被包含)
- 插入操作的过程主要是使用多个 HASH 函数将 Key 映射到一个位向量中的多个位置,并将这些位置的位设置为 1。
- 检查该 Key 是否存在时则仍先把 Key 给 HASH 到多个位置,如果所有的位置对应的位的值都为 1,那么说明该 Key 大概率存在。如果不全为 1,则该 Key 肯定不存在。
- 布隆过滤器在 LSM 中最主要的应用,可以在磁盘组件的基础上进行构建从而显著提高点查询的性能。要扫描磁盘组件时,首先查询布隆过滤器,如果布隆过滤器判断该 Key 存在时才对应地去搜索磁盘组件对应的数据结构,如 B+ 树。还可以将布隆过滤器应用到具体的叶子节点对应的 Page 上。一个点查询首先通过查询 B+ 树查询非叶子节点页(非叶子节点页应该尽可能小,便于缓存在内存中加速检索),对应的定位到叶子节点的 Page,在真正执行取页之前首先利用布隆过滤器判断该页中是否包含该 Key,如果不包含则对应地不取该页,从而减少磁盘 IO 次数。由于布隆过滤器是概率型数据结构,还是会有不存在的Key检索引起不必要的IO操作的现象,量化方式可以参见原文,通常使用 10bits/key 作为默认配置,对应的错误率约为 1%。
- 布隆过滤器由于其所占存储空间较小,通常会被缓存在内存中来减小查询过程中的 IO 次数。
Partitioning
- 另一个常用的优化方法是将 LSM 树的磁盘组件划分为多个(通常是固定大小的)小分区,LevelDB 中的 SSTable 文件就是如此。
- 优势在于,首先,分区将大型组件合并操作分解为多个较小的操作,限制每个合并操作的处理时间以及创建新组件所需的临时磁盘空间,此外,分区可以通过仅合并具有重叠键范围的组件来适应顺序创建键或 skewed updates 的工作负载。对于顺序创建的键,基本上不执行合并,因为不存在键范围重叠的组件;对于 skewed updates,具有冷更新范围的组件的合并频率可以大大降低。传统的 LSM Tree 的滚动合并机制已经利用了分区的优势,然而,由于其滚动合并的实现复杂性,目前的 LSM-tree 实现通常选择实际的物理分区,而不是滚动合并。
- LSM 树的分区应用中常常使用到了 PE[7] 文件,一个 PE 文件包含很多分区,每个分区在逻辑上可以被看作是一个独立的 LSM 树,当一个分区变得太大时,可以将它进一步划分为两个分区。但是,这种设计强制了分区之间严格的键范围边界,降低了合并的灵活性。
- 至于当今的 LSM-tree 实现中使用的分区优化,需要注意的是,分区与合并策略是正交的;可以调整 Leveling Merge Policy 和 Tiering Merge Policy (以及其他新兴的合并策略)来支持分区。据我们所知,只有分区调平策略 partitioned leveling policy 被工业的基于 LSM 的存储系统(如LevelDB[8] 和 RocksDB[9] )完全实现。最近的一些论文提出了不同形式的分区分层合并策略,以获得更好的写性能。
- 由 LevelDB 提出的分区 Leveling Merge Policy 中,每一层的磁盘组件被分成了确定大小的 SSTables。如图所示,其中 Level0 由于直接是内存刷回的,所以没有进行分区,这种设计还可以帮助系统吸收写突发,因为它可以在 Level0 容忍多个未分区组件,要将一个 SSTable 从 Level L 合并到 Level L + 1,需要选择它在 Level L + 1 上的所有重叠的 SSTable,将 SSTables 与它合并,生成仍然处于 Level L + 1 的新 SSTables。以图为例,Level1 层的范围为 0-30 SSTable 要和 Level2 层的范围分别为 0-15 和 16-32 SSTables 进行合并。合并之后在 Level2 层上的分布则为 0-10,11-19,20-32;旧的 SSTable 将被垃圾回收,可以使用不同的策略来选择下一步在每个级别合并哪个 SSTable。LevelDB 利用了轮询的机制来减小总的写开销。RocksDB 选择要压缩的文件方式为:https://github.com/facebook/rocksdb/wiki/Choose-Level-Compaction-Files

- 分区优化方案也可以应用到 Tiering Merge Policy 中,这样做的一个主要问题是,每个级别可能包含多个具有重叠键范围的SSTables。必须根据最近的时间对这些 SSTables 进行适当的排序,以确保正确性。可以使用两种可能的方案来组织每个级别的SSTables,即垂直分组和水平分组。
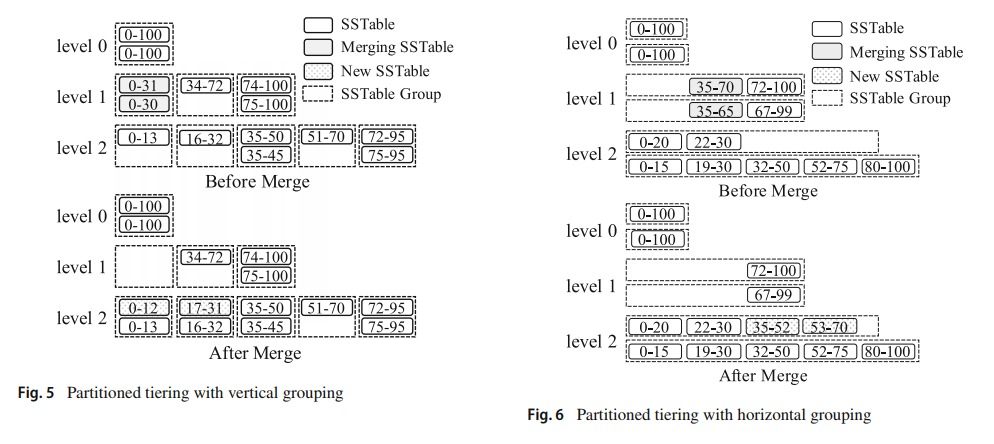
- 垂直分组方案将具有重叠键范围的 SSTables 分组在一起,从而使组具有不相交的键范围。可以理解为 Leveling Merge Policy 的扩展来支持 Tiering。如图所示,垂直分组是将具有重叠键范围的 SSTables 分为一组,然后不同的组之间范围不重叠,在合并操作期间,将组中的所有 SSTables 合并在一起,根据下一层重叠组的键范围生成结果 SSTables,然后将这些键范围添加到这些重叠组中。举例说明就是,图中 Level1 里的第一组的 0-31 和 0-30 的两个 SSTable 文件合并到了一起生成 0-12 和 17-31 两个新的 SSTable 文件,然后将被添加到 Level2 中具有重叠键的组中。在合并之前,0-30 和 0-31 两个 SSTable 有重叠的键范围,点查询对这两个 SSTable 都将进行扫描,然而在合并之后,变成了 0-12 和 13-31 两个不重叠的 SSTable,点查询将只会扫描其中一个 SSTable 文件。还应该指出,在这个方案下,SSTables 不再是固定大小的,因为它们是根据下一层重叠组的键范围产生的。
- 而水平分组方案中,每个逻辑磁盘组件都被分区到一组 SSTables 中,直接作为一个组,这允许基于 SSTables 单元增量地形成磁盘组件。通过将水平分组划分为一组固定大小的 SSTables,直接充当逻辑组,每一层都会包含一个活跃的 group,也适用于接收上层发送的需要合并的 SSTable 数据的第一个组,在未分区的情况下,这个活动组可以看作是在 L - 1 级合并组成的部分组件,合并操作从某个级别的所有组中选择具有重叠键范围的SSTables,并将生成的 SSTables 添加到下一个级别的活动组中。如图中的例子所示,Level1 的 35-70 和 35-65 SSTables 被合并到一起,新生成的 35-52 和 53-70 被添加到 Level2 中的第一组中。即便在水平分组方案中的 SSTable 大小是固定的,组中的一个SSTable可能会与其余组中的大量SSTable重叠,这仍然是可能的。
Concurrency control and recovery
- 对于并发控制,LSM-tree需要处理并发读和写,并处理并发刷新和合并操作。确保并发读写的正确性是数据库系统中访问方法的一般要求。根据事务隔离需求,目前的 LSM-tree 实现要么使用加锁的方式,要么使用多版本控制。多版本控制方案能在 LSM 中比较好地进行应用,因为针对旧版本的 Key 和数据,可以利用垃圾回收机制进行垃圾回收。而并发的刷新和合并操作是 LSM 系统独有的操作,这些操作会修改 LSM Tree 的元数据,如活跃的组件列表等。因此,访问组件元数据的操作必须正确地进行同步,为了避免一个正在被使用的组件被删除,每个组件必须维护一个计数器进行引用计数,在访问一个组件之前,查询操作必须获取组件的快照并对该组件的使用计数进行+1操作。
- 因为所有的写操作首先都是先写入到内存中,WAL 机制主要用于保证数据的持久化。为了简化数据的恢复流程,现有系统通常采用无窃取缓冲区管理策略。也就是说,只有在所有活动的写事务都已终止时,才能将内存组件刷回,在对 LSM-tree 进行恢复期间,将重播事务日志以 redo 所有成功的事务,但是由于使用了no-steal策略,所以不需要撤消 undo。同时,在发生崩溃时,还必须恢复活动磁盘组件的列表。对于未分区的 LSM Tree,可以通过向每个磁盘组件添加一对时间戳来实现,该时间戳指示所存储条目的时间戳范围,此时间戳可以简单地使用本地时钟时间或单调递增的序列号生成,要重构组件列表,恢复过程只需找到所有具有不相交时间戳的组件,如果多个组件具有重叠的时间戳,则选择时间戳范围最大的组件,其余的则可以简单地删除,因为它们将被合并形成所选的组件。对于分区 LSM Tree,使用一种传统的方式,在 LevelDB 和 RocksDB 中广泛应用的方式,即维护一个单独的元数据日志文件来存储所有结构型元数据的变化,例如添加和删除 SSTables。在故障恢复时可以通过重播元数据日志文件来恢复 LSM Tree 的结构。
- redo log 和 undo log 区别: https://zhuanlan.zhihu.com/p/35574452
开销分析
为了理解 LSM Tree 在性能上做的权衡,我们可以通过分析写操作,点查询,范围查询和空间放大带来的开销。衡量写和查询的开销的方式是统计每一次操作对应的磁盘 IO 次数,此处针对未分区的 LSM Tree 进行了分析,同时讨论了开销最大的情况。
预先假设
- 假设 LSM Tree 有 L 层。每一层之间的大小比例为 T,对于一个稳定的 LSM Tree 来说(稳定是指插入和删除的数据大小相等),L 通常是不变的。假设 B 为页的大小,即每个数据页可以存储的 KV 条目数,假设 P 是内存组件中的页数。所以内存组件中最多包含 B*P 个键值对,那么第 i 层中将包含最多 $T^{i+1} * B * P $ 个键值对。给定 N 个键值对,那么最大层大约有 $ N * \frac{T}{T+1}$ 个键值对,因此建立等式,可以得到层数大约为以 T 为底的 。
写开销
写开销(部分文献以写放大来衡量)主要是指插入一个键值对到 LSM Tree 中的平均开销,应该注意的是,这个成本度量了将这个条目合并到最大级别的总体 I/O 成本,因为将一个条目插入到内存中不会导致任何磁盘 I/O。
- 在 Leveling Merge Policy 中,每一层的组件在被该层数据满之前都会被合并 T - 1 次,然后传到下一层
- Tiering Merge Policy 中每一层的多个组件只会合并一次然后直接传到下一层。
- 因为每一个页包含 B 个键值对,每一个键值对的写开销对于 Level 方案将为 O(),对于 Tiering 策略将为 O()
点查询开销
- 查询的 IO 开销将取决于 LSM Tree 的组件数量。如果没有布隆过滤器,点查询的 IO 开销将为 O(L) Level 和 O(T * L) Tiering,然而布隆过滤器也可能提高点查询的开销,诸如一些无效的查询,查询一些不存在键对应的数据,布隆过滤器将增加查询的开销。假设所有的布隆过滤器都有 M 个 bit 位,每一层都有相同的误报率,N 个 Key,每一个布隆过滤器的误报率约为 ,那么无效查询的开销约为 对于 Level - ,对于 Tiering - 。而至于查询有效的 Key,至少要执行一次 IO 操作才能得到对应的键值对。实际应用中布隆过滤器的误报率远小于 1,所以一次成功的点查询开销无论是 Level 还是 Tiering 均为 O(1)
范围查询开销
- 范围查询的开销取决于查询范围的选择,假设一次范围查询访问的 Key 的数量为 s,如果 ,则认为该范围查询较 long,否则较 short。差别主要为 long range query 的开销主要受最高 Level 影响,因为最高 Level 包含所有数据的绝大部分,而相对而言 short range query 会受每一层的影响,因为查询会向每个磁盘组件发起一次 IO。因此 long range query 的开销为 Level - 和 Tiering - 。short range query 的开销约为 Level - O(L) 和 Tiering - O(T * L)
空间放大系数
- 我们量化了 LSM Tree 中的空间放大,空间放大即为最终的键值对总数除以键值对单位数。Level 中,最糟糕的情况为所有的数据都位于 L - 1 层时,大约包含总数据量的 1 / T,此时更新数据然后写入到 L 层,因此该情况下的空间放大系数为 。而对于 Tiering,最坏的情况为在最高层额磁盘组件都包含相同的键集合,此时的空间放大系数将为 。实际环境中,空间放大是一个部署存储系统过程中需要考虑的重要的因素,因为它直接决定了在给定负载的情况下的存储开销。
总结

- 通过总结不同合并策略下的 LSM Tree 的开销,可以观察到层级之间的大小比例 T 对开销的影响。对于 Leveling,通过每层维护一个磁盘组件,使得查询性能和和空间放大方面表现较好,但因为磁盘组件不可避免地需要经常进行合并,所以写性能上将严重受层级比例 T 的影响。相比之下, Tiering 的合并策略,主要时在每层维护 T 个磁盘组件,写性能表现较好,但对应地其查询性能和空间放大的开销都会严重受层级比例 T 的影响。 LSM Tree 是具有很大的调整空间的,例如改变合并策略从 Leveling 到 Tiering,可以极大地提高写性能,但对点查询的负面影响因为布隆过滤器的应用可以变得很小,但是,范围查询和空间利用率将受到显著影响。最近关于改进 lsm tree 的文献中的每种方法都要进行一定的性能权衡,主要是在读开销 R, 写开销 U 和存储开销 M 上进行权衡。
LSM-Tree 的优化方案
我们提出了一个分类法,用于对现有的改善lsm树的研究工作进行分类。然后,我们提供了LSM-tree文献的深入调查,这些文献遵循了提出的分类法的结构。
LSM Tree 改进方案的分类
尽管LSM-tree在现代NoSQL系统中非常流行,但是基本的LSM-tree设计却存在着各种各样的缺陷和不足。现在,我们确定了基本LSM-tree设计的主要问题,并根据这些缺陷进一步提出了LSM-tree改进的分类。
优化方案的分类
- 写放大:尽管 LSM Tree 相比于如 B+ 树这种就地更新的数据结构可以提供更好的写性能,因为减少了随机 IO,即便是在 LevelDB 和 RocskDB 中广泛应用的 Leveling 合并策略,仍然会引起相对较为严重的写放大问题,严重的写放大问题不仅限制了 LSM Tree 的写性能,也因为频繁的磁盘写操作减少了 SSD 的寿命,大量的研究致力于减小 LSM Tree 的写放大问题。
- 合并操作:合并操作对于 LSM Tree 的性能影响至关重要,因此需要仔细实现,另外,合并操作可能还会给整个系统带来负面影响,包括在大量合并过程后出现的缓冲区缓存不命中(合并之后导致的缓存失效)。一些优化方案在合并策略上做了一些改进来解决合并过程带来的性能问题。
- 硬件:为了最大化性能,LSM Tree 必须仔细实现以充分利用硬件平台。传统的 LSM Tree 是基于磁盘设计,目标为减少随机 IO。近年来,新的硬件平台给数据库系统提出了新的机会以实现更好的性能,所以最近大量研究致力于通过充分利用硬件平台来提升 LSM Tree 的性能,主要涉及大内存、多核、SSD/NVM 和 native storage。?
- 特殊负载:针对确定特殊负载的优化也能实现较好的性能,需要根据负载的特征对 LSM Tree 进行调整和定制。
- 自动调整:基于 RUM [10]猜想,没有方法可以同时对读、对写和对空间利用率进行优化。对于给定的工作负载,LSM 树的可调优性是实现最佳权衡的一个很有前途的解决方案,然而,由于有太多的调优选项和参数,例如内存分配、合并策略、大小比等,所以很难对 LSM 树进行调优。为了解决这个问题,文献中提出了几种自动调优技术。
- 二级索引:给定的 LSM-tree 只提供一个简单的键-值接口。为了支持对非键属性的查询的有效处理,必须维护辅助索引。该领域中一个问题就是如何高效地维护一组关联二级索引,且在写性能方面损耗较小。各种基于 LSM 的二级索引结构和技术也进行了设计和测试。
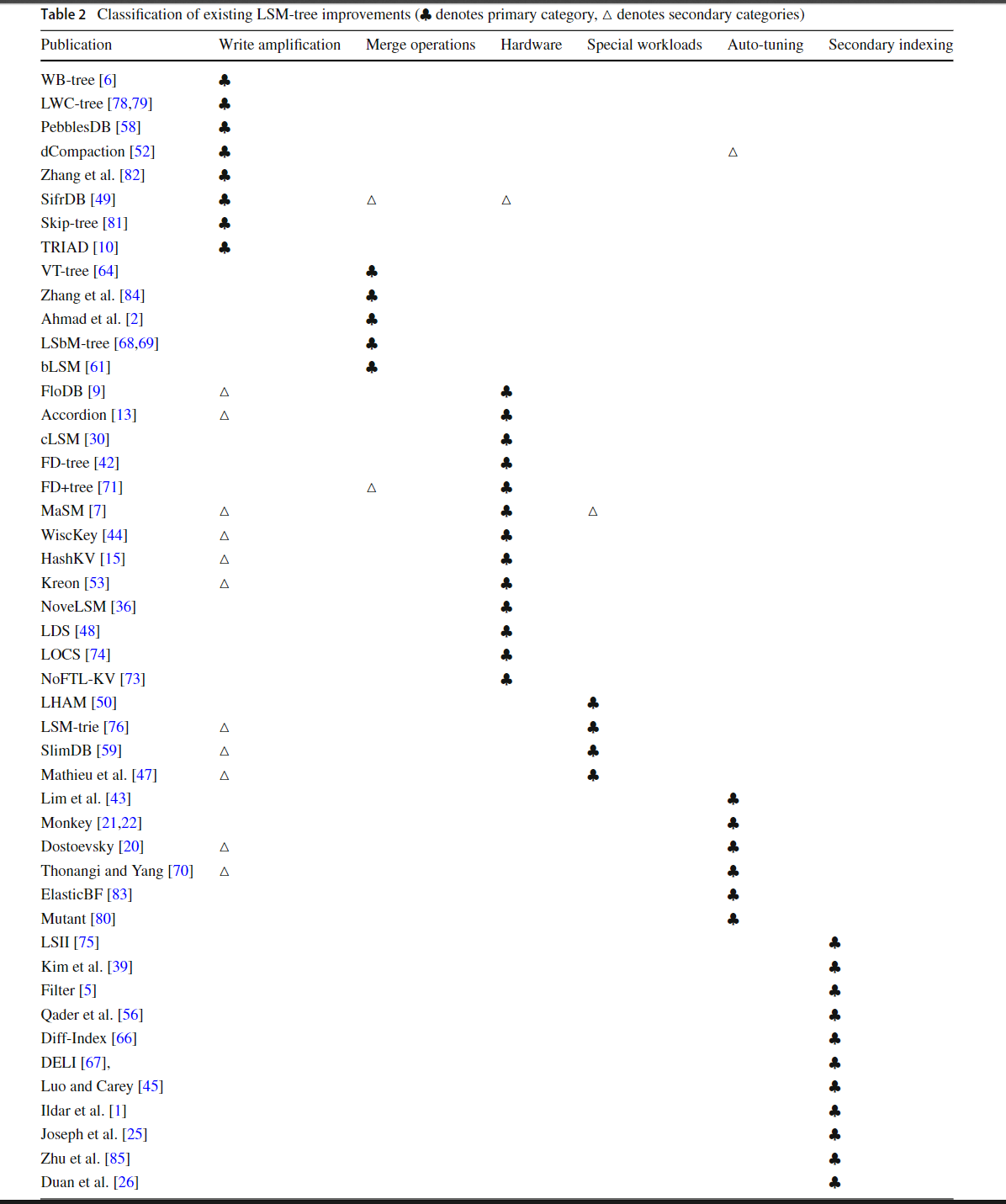
基于这些针对基础 LSM Tree 设计的主要问题,我们提出了一种分类方法来强调现如今的研究试图优化的方向,如图所示。根据这种分类,表2 进一步根据每个改进的主要和次要关注点对LSM-tree改进进行了分类
.jpg)
减小写放大
- 在本节中,我们将回顾文献中旨在减少 LSM 树写放大的改进。大多数这些改进都是基于 Tiering 的,因为 Tiering 的写性能比 Leveling 好得多。其他提出的改进已经开发了执行 Merge Skipping 或利用数据倾斜的新技术。
Tiering
从前文的叙述中。我们可以知道 Tiering 的比 Leveling 的写放大系数更小,但是会导致更差的查询性能和空间放大问题。基于 Tiering 的优化方案基本都是在第 2.2.2 节提到的水平或垂直分区 Tiering 设计基础上进行了一定的修改优化。Partitioned tiering with vertical grouping 或者 Partitioned tiering with horizontal grouping

-
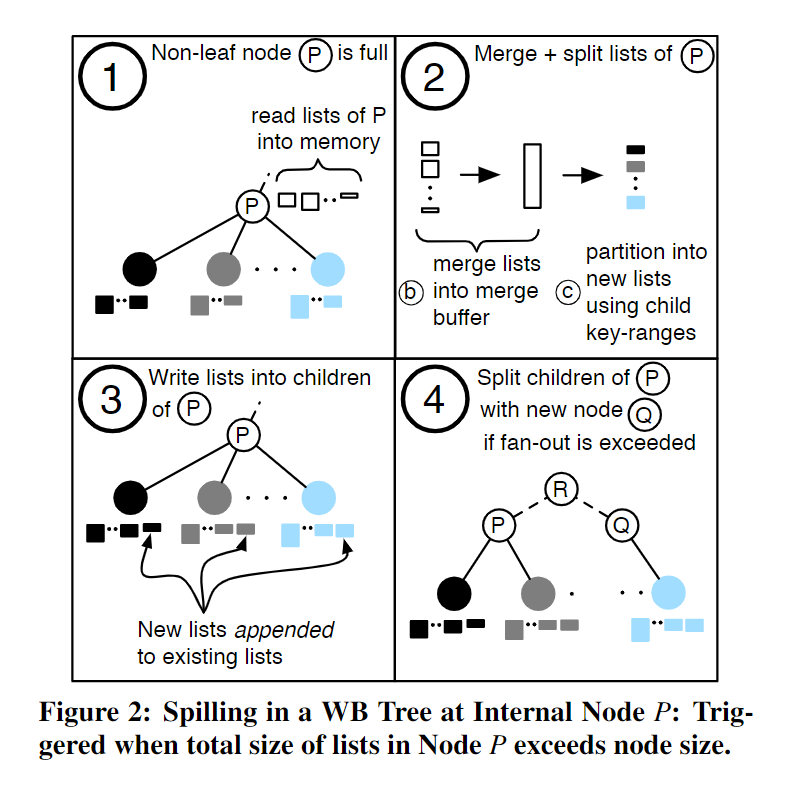
WriteBuffer Tree(WB-Tree):一种垂直分组 Tiering 设计的变体。主要做了以下修改,首先,利用 HASH 分区来实现了负载均衡,从而使得每个 SSTable Group 存储等量的数据;其次,该方案将 SSTable Group 组织成一个类似于 B+ 树的结构来利用 B+ 树的自平衡来减小 LSM 树的层数。具体而言,每一个 SSTable Group 将被当作一个 B+ 树中的节点。当一个非叶子节点满了之后,即拥有了 T 个 SSTable 之后,这 T 个 SSTables 将合并到一起形成新的将要被添加到其子节点中的 SSTables;当一个叶子节点满了之后,将合并后的 SSTables 按照范围拆分成两个叶子节点,所以每个叶子节点将会收到大约 T/2 个 SSTables。
%5D(undefined).jpg)
-
Lightweight Compaction Tree(LWC-Tree):同样是垂直分组 Tiering 设计的变体,进一步提出了一种实现 SSTable Group 负载均衡的方法,回顾前文中提到的垂直分组模式下,SSTable 不再时严格固定大小的,因为 SSTable 是基于下一层的重叠键范围产生的。该方案中,如果一个 Group 包含了太多键值对,将在该组被合并之后缩减改组的范围并扩充其兄弟 Group 的范围来实现负载均衡。
-
PebblesDB:垂直分组 Tiering 设计的变体,主要的不同是该方案收跳表的启发使用了 Guard(哨兵)的思想来确定 SSTable 的键范围。Guards ,即 SSTable 的键范围,将基于插入的键被概率性地选择,从而实现负载均衡。一旦一个 Guard 被选中,他将在下一次合并过程中被应用。PebblesDB 进一步实现了 SSTables 的并行查询来提升范围查询的性能。
-
dCompaction:引入了虚拟的 SSTable 和虚拟的合并操作以减少合并的频率。一个虚拟的合并操作生成虚拟的的 SSTable,该 SSTable 可能指向多个实际输入的 SSTables,但不执行真正的合并操作。但因为一个虚拟的 SSTable 指向了具有重叠键范围的多个实际 SSTables,查询性能将有一定的损失。为了解决这个问题,dCompaction 基于实际的 SSTable 数量引入了一个阈值来控制触发实际合并操作的时机。如果查询过程中发现一个虚拟 SSTable 指向太多 SSTables,也是会触发合并操作的。总之,dCompaction 方案就是将合并操作进行了延迟直到多个 SSTables 可以被合并到一起时,因此该方案可以被看成 Tireing 合并策略的变体。
-
以上描述的四种方案都是基于相似的结构,垂直分组 Tiering 设计,区别主要在于负载均衡的实现方式。例如 WB-Tree 使用了 HASH,但也就在范围查询方面做了舍弃。LWC-Tree 动态调整了 SSTable Group 的范围,PebblesDB 依赖概率性的 Guards 机制。相比之下,dCompaction 不提供内置的结构来实现负载均衡,而使用算法层面的优化策略来实现。不清楚倾斜的 SSTable Group 如何影响这些结构的性能,需要进一步的研究来理解这个问题并测试这些负载均衡策略。
-
Zhang et al. 和 SifrDB 则是基于水平分组 Tiering 设计的。SifrDB 还提出了一种早期清理技术,以减少合并期间的磁盘空间利用率。在合并操作期间,SifrDB 增量地激活新生成的SSTables,并停用旧的 SSTables。SifrDB 进一步利用 I/O 并行性,通过检查多个 SSTables 来提高查询性能。
Merge Skipping
- skip-tree:提出了一种 Merge Skipping 的想法来提升写性能。传统的 LSM Tree 中,观察结果是,每个条目必须从0级向下合并到最大级别。如果某些条目可以通过跳过逐层合并直接推到更高的级别,这样总写成本就会降低。如下图所示,在 L 级的合并过程中,skip-tree 直接将一些键推入 L + K级的可变缓冲区,这样就可以跳过一些逐级合并。同时,在随后的合并过程中,可调缓冲区中的跳过项将与L + K 级别的 SSTables 合并。为了确保正确性,只有在 L +1 到 L + K - 1 的任何一个中间级别中都没有出现该键时,才可以将该键从 L 级推到 L + K 级。如何判断中间层是否存在该键,可以通过每一个 Level 总的布隆过滤器进行高效地判断。该方案进一步实现了写前日志 WAL 来保证存储在可变缓冲区中的数据的持久性。为了减小日志的开销,skip-tree 只记录了 key 和原始 SSTable 的 ID,同时要避免 SSTable 被删除,如果该 SSTable 被可变缓冲区中的任何 Key 所引用的话将不能删除该 SSTable。即便 skip-tree 是一个在减小写放大方面很有意思的一个方案,但该方案为了管理可变缓冲区引入了较高的实现复杂度。此外,该方案本质是减少中间层的合并,还不清楚相比于可调 LSM Tree 中的减小大小比例的效果如何。

Exploiting data skew
- TRIAD:针对倾斜更新负载减小了写放大,倾斜更新负载是指一些热点数据经常被更新。主要思想是在内存组件中将冷热数据键进行分离,从而保证只有冷数据键会被刷回到磁盘组件中。所以,当热数据键被更新时,该键对应的老版本的数据可以直接被丢弃,不用写回到磁盘。即便热数据没有刷回到磁盘,但是回周期性地拷贝到新的事务日志中,老的事务日志就可以进行回收。该方案也通过采用延迟 Level0 层的合并操作(直到 Level 0 含有许多 SSTables)来减小写放大。该方案提供了一种优化,避免在刷新之后创建新的磁盘组件,取而代之的是,事务日志被当作磁盘组件并在其上构建索引结构提升查询性能。然而,范围查询性能仍然会受到消极的影响,因为存储再日志文件中的键值对不是有序的。
总结
- 这类中的所有改进,以及后面几节中的一些改进,都声称它们可以极大地提高 LSM Tree 的写性能,但是它们的性能评估常常没有考虑到 LSM Tree 的可调性。也就是说,这些改进主要是针对 LevelDB 或RocksDB 的默认(未调优的)配置进行评估的,它们使用大小比为 10 的 leveling 合并策略。目前还不清楚这些改进与可调的 LSM-trees 相比效果如何。为了解决这个问题,一个可能的解决方案是调整 RocksDB 的参数(调整层级之间的大小比例或者采用 Tiering 合并策略) 以实现与上文提到的优化方案基本相同的写吞吐量,然后测试这些优化方案提高查询性能和减小空间放大的效果。此外,这些优化方案主要研究了查询性能,空间放大问题往往被忽视。这将是一个有用的实验研究,以充分评估这些改进与调优的基线 LSM Tree,以评估它们的实际用途。我们也希望在未来的研究中可以避免这种情况,在评估所提出的改进时考虑 LSM 树的可调性。
优化合并操作
提升合并性能 Improving merge performance
- VT-tree:提出了一种改进合并性能的拼接方法。基本思想是,在合并多个SSTables时,如果一个页面的键范围来自一个输入 SSTable,且该 数据页 和来自别的 SSTable 的数据页的键范围没有重叠时,就可以让 SSTable 简单地指向这个页面,而无需再次读取和复制。尽管拼接可以提高某些工作负载的合并性能,但它也有一些缺点。首先,因为数据页不再连续第存储在磁盘上,很容易产生碎片。为了减小碎片化,VT-tree 引入了一个拼接阈值 K,当至少有来自同一个 SSTable 的 K 个连续的页时,才会触发拼接操作。此外,因为合并过程中,拼接的页中的键不再会被扫描,对应的布隆过滤器也不会被创建,为了解决这个问题,VT-tree 使用了 quotient filters,因为多个 quotient filters 可以直接组合而不需要访问原始键。
- **Zhang et al. **:提出了一种流水线的合并操作实现从而更好地利用 CPU 和 IO 的并行性来提升合并性能。观察发现合并过程包含很多个阶段,包括读阶段、归并排序阶段和写阶段,读阶段从输入的 SSTables 中读取数据页,在归并排序阶段,读出来的数据页将被归并排序并生成新的数据页,最后在写阶段新的数据页将被写回磁盘。因此,读阶段和写阶段过程中,IO压力比较大,而归并排序阶段,CPU压力较大。为了更好地利用 CPU 和 IO的并行性,提出了一种方案将上述三个阶段的执行流水线化,如图所示。在该例中,在第一个输入页被读取之后,该方法持续地读第二个输入页(利用磁盘),第一个数据页相应地执行归并排序(利用CPU)。

减小缓冲缓存不命中 (提升缓存命中率)
- 合并操作会对系统的缓存行为产生影响,当生成新的组件时,查询操作可能会经常出现缓存miss的情况,因为新组件还没来得及缓存,简单的write-through缓存策略没法解决这样的问题。新组件的所有数据页都将在合并操作中被缓存,从而导致缓存中其他有效的数据页可能被淘汰,这些数据页被淘汰之后又会造成缓存不命中。
- Ahmad et al 研究了合并操作对整个系统的性能影响,研究表明合并操作会消耗大量的 CPU 和 I/O 资源,并在查询响应时间方面带来极大的开销。为了解决这个问题,该方案提出通过 offload 合并操作放在远程服务器上执行以减小影响,合并操作完成后,设计一个智能的缓存预热算法来获取新组件的数据从而减小缓存丢失率。核心思想是增量地切换到新组件,一个块接着一个块,以便顺利地将传入的查询从旧组件重定向到新组件。最终,缓冲缓存未命中的突发被分解成大量的更小的突发,从而最小化了组件切换对查询性能的负面影响。
- LSbM-tree:上述方法的局限是合并操作必须卸载到独立的服务器上,随后发现,由于新生成的页面和现有的热页面之间存在争用,仅使用缓存增量预热算法是不够的,为了解决这个局限,新提出了方案LSbM-tree。如图所示,L 层的 SSTable 合并到 L+1 层时,老旧的 L 层的 SSTable 将不会被立马删除而是追加写入到事先分配给 L+1 层的缓冲区中,L+1 层的就SSTable 将不会被追加到缓冲区中,因为此时 L+1 层的旧 SSTable 的数据是来自于更上层的,且已经被缓存过。查询的时候将会检索到被缓存的 SSTable 以提升缓存命中率,同时根据这些缓存中的 SSTable 的访问频率渐渐被删除,该方法不会造成任何额外的磁盘IO,因为该方案只是延迟了老 SSTable 的删除时机。然而该方法只针对那种只有小部分的数据会被经常访问的倾斜负载比较有效。对于没有被缓存的冷数据反而会引入额外的访问开销,尤其是那些不能使用Bloom过滤器判断的操作,如范围查询。

最小化Write Stalls(写停顿)
- 尽管 LSM 相比于 B+ 树提供过了很高的写吞吐量,但因为后台任务中大量繁重的操纵如刷回、合并等,LSM 经常会出现写停顿以及一些不可预知的写延迟。
- bLSM:该方案针对未分区的 leveling 合并策略提供了一种 spring-and-gear 的合并调度器,以尽可能减少写停顿。它的基本思想是在每个 Level 上引入一个额外的组件,以便在不同 Level 上的合并可以并行进行,而合并调度器控制整个合并的过程以确保 Level L 生成新组件(要合并到 Level L+1 中的组件)的过程在 Level L+1 上执行的合并完成之后进行。这最终会限制内存组件的最大写速度,从而减少大量的写停顿。但是,该方案也有自己的局限,即仅针对未分区的 leveling 合并策略;该方案只是限制了写入内存组件的最大延迟,而队列延迟(通常是性能变化的主要来源)被忽略了。
总结
- 该分类下针对 LSM Tree 的优化方案主要表现在对合并操作的优化,主要涉及性能、缓存命中率和写停顿等方面。VT-Tree 为了避免输入数据页的复制引入了拼接操作,但可能引入较多对硬盘不友好的碎片,同时该方案与布隆过滤器不兼容。Pipelined merge 通过利用 CPU 和 IO 的并行性较大地提升了合并性能,业界中也已经有很多优化方案使用了流水线相关技术,通过利用磁盘的预读和延迟写等操作。
- Ahmed et al. 和 LSbM-tree 则展示了两种缓解由于合并操作造成的缓存不命中的方法,但两种方法都有较为明显的局限,前者需要专门的服务器做合并操作,后者延迟了老旧组件的删除可能会给冷数据的查询带来额外的性能开销。
- 写停顿是 LSM Tree 中独有的问题,因为其异地更新的机制。bLSM 是唯一在该问题上做研究的方案,但是该方案只是限制了内存组件的最大写延迟,端到端的延迟还是有很大的变数,因为其中排队延迟占了较高的比重。
基于新硬件的优化
- LSM 的优化方案对应的硬件平台大致有大容量内存、多核、SSD/NVM 以及本地存储。基于硬件的优化方案都遵循着一种范式----修改 LSM 的基础设计从而尽可能地利用硬件平台的性能。
大容量内存
- 大容量内存肯定是有效的优化方案,不仅能减少 LSM 的磁盘组件层级数,在读写性能方面都能有很大提高。但是,对大容量内存场景下的内存组件的管理也面临着一些挑战。如果内存组件是直接使用的堆上数据结构来实现的话,大容量内存可能会产生大量的小对象,导致频繁的GC操作。相反,如果使用堆外数据结构实现的话,例如并发 B+ Tree,大容量内存会导致较大的查询开销,因为大容量内存意味着 B+ 树的深度会很大,在写的时候也可能造成大量的 CPU 缓存不命中等情况,因为写操作必须先查询到对应地址。
- FloDB:设计了一个两层结构来管理内存组件,上层是一个较小的 HASH 表来支持快速写,下层是一个大的跳表来支持高效的范围查询。HASH 表满了之后,将使用一个批处理算法将键值对高效地迁移到跳表中。通过将随机写限制在很小的一个内存区域,显著地提高了内存中的写吞吐量。FloDB 要求范围查询必须等待哈希表被清空,以便仅搜索跳表来响应查询。然而存在两个主要的问题,对于同时包含写操作和范围查询的负载,因为可能存在写操作和范围查询操作频繁切换的情况,所以该方案对这种负载的优化效果不好。其次,跳表可能占用大量的内存空间,导致内存的利用率不高。
- Accordion:为了解决 FloDB 方案中的问题,该方案设计了一个多层的架构来管理内存组件。如图所示,设计了一个很小的 mutable 内存组件在最上层来处理写操作,当该层满了以后,不刷到磁盘,而是使用一个内存中的 flush 操作刷入到 immutable 内存组件,相似地,immutable 内存组件也可以在内存中进行合并操作来提高查询性能,并回收老旧的键值对对应的空间(垃圾回收)。需要注意的是,内存中的刷回和合并操作不会引入任何磁盘 IO,所以通过利用大容量内存可以降低磁盘 IO 开销。

多核
- cLSM:针对多核机器进行了优化,并针对不同的 LSM 操作提供了新的并发控制算法。该方案将 LSM 组件放置在一个并发链表中以减小由于同步操作造成的阻塞。刷回和合并操作经过精心设计,因此它们只会对链表进行原子性修改,而不会阻塞查询。当内存组件满了之后,在内存组件将被刷回的时候会创建一个新的内存组件。为了避免此时的写操作将数据插入到旧的内存组件中,写入操作在进行修改之前需要获取一个共享锁,刷回线程在刷回之前需要一个独占锁。cLSM 通过多版本控制和原子读-修改-写操作进行快照扫描,并使用乐观并发控制方法,该方法利用了所有写操作都涉及到内存组件这一事实。
SSD/NVM
- 区别于传统的机械硬盘只是在顺序 IO 方面表现高效,以 SSD/NVM 为代表的新型存储设备在随机 IO 方面也表现较好。NVM 还提供了高效的字节寻址随机访问策略,并提供了数据持久化保证。
- FD-tree:使用了一个类似 LSM Tree 的设计来减小 SSD 上的随机写操作。一个主要的区别是FD-tree利用分级级联来提高查询性能,而不是使用Bloom过滤器。对于每一层的组件,FD-tree还存储了指向下一层每个页面的指针。如图12所示,Level 1 的键 1、27、51、81 指向了 Level 2 的数据页。在 Level 0 层执行了一个二分查找之后,查询操作可以通过指针遍历所有的层级。然而该方案为合并操作引入了额外的复杂度,Level L 的组件合并到 L+1 层时,所有 0 到 L-1 层也都必须合并从而才能重建对应的页面指针。但由于没有了布隆过滤器,对于不存在的键的点查询可能就会造成磁盘 I/O。正是因为这些原因,现代 LSM Tree 的设计都更喜欢采用 BloomFilter 而不是 分级级联。

- FD+tree:主要提升了 FD-Tree 中的合并性能。当从 Level 0 向 Level L 合并时,FD-Tree 的方案导致Level 0 到 Level L 层都需要创造新组件,将临时导致空间放大问题。为了解决这个问题,FD+tree 增量地激活新组件,并从没有被任何活跃的查询操作使用的旧组件中回收页面。
