- SIGMMOD18 Dostoevsky: Better Space-Time Trade-Offs for LSM-Tree Based
Key-Value Stores via Adaptive Removal of Superfluous Merging
Abstract
- 无论是学术界还是工业界,所有主流的基于 LSM 树的键值存储都在更新的 I/O 成本和查询和存储空间的 I/O 成本之间进行了权衡。因为在所有的 LSM Tree 的级别上都需要执行 Compaction 操作来限制查询遍历的 runs,并删除 obsolete 的数据项来腾出存储空间。即便是最先进的 LSM Tree 设计,来自 LSM Tree 所有层次的合并操作(除了最大的层次)减少的点查询成本、大范围查询成本和存储空间,减少的效果可以忽略不计;与此同时还增加了更新操作的平摊开销。
- 为了解决这个问题,我们提出了 Lazy Leveling,一种新的设计,从除开最大层以外的所有 level 中删除合并操作。同时提出了 Fluid LSM-tree,一种可以涵盖整个 LSM-tree 设计领域的通用设计,可以参数化以假设任何现有的设计。相对于 Lazy level, Fluid LSM-tree 可以通过在最大级别上合并更少的内容来优化更新,或者通过在所有其他级别上合并更多内容来优化小范围查询。
- Dostoevsky,一种键值存储,通过基于应用程序工作负载和硬件来动态调整的弹性的 LSM-tree 设计,自适应地消除多余的合并。基于 RocksDB 实现,测试表明无论是性能还是存储空间方面都优于目前最先进的设计。
Introduction
- LSM-tree 将要插入/更新的条目缓冲在内存中,并在缓冲区填满时将缓冲区作为 sorted run 刷新到次要存储。LSM-tree 稍后对这些 runs 进行排序合并,以限制查找必须扫描的run 数量,并删除过时的条目。LSM-tree 将运行组织成指数级增长的容量,更大的级别包含更老的运行。当条目被替换更新时,点查找通过从最小到最大的级别查找条目的最新版本,并在查找目标键时终止查找。另一方面,范围查找必须在所有级别的所有 run 中访问相关的键范围,并从结果集中删除过时的条目。为了提高单个 run 的查询速度,设计中常常包含了两个额外的内存中的数据结构。首先,对于每个 run,都有一组包含每个 run 块的第一个键的 fence 指针,这允许查找在一个 run 中只使用一个 I/O 就可以访问特定的键;第二,每个 run 会有一个 BloomFilter,这允许点查询跳过不包含目标键的 runs。这个设计被应用到了大量的现代 KV 存储中,如 LevelDB、BigTable 等。
- 问题:LSM-tree 中的合并操作的频率控制了在 更新的 I/O 成本 和 查询和存储空间放大的 I/O 成本之间的 trade-off,另外的问题就是现有的设计在这些指标之间的 trade-off 并不理想。下图表示了指标之间的权衡关系,虽然这些 y 轴指标具有不同的单位,但它们相对于 x 轴的权衡曲线具有相同的形状。两个极端分别是 log 和 sorted array。LSM-tree在完全不合并或尽可能多地合并时,分别退化为这些边缘点。我们将主流系统放置在这些边缘点之间的顶部曲线上,基于它们的默认合并频率,我们为 Monkey 绘制了一个优越的权衡曲线,我们证明了存在一个甚至比Monkey更好的权衡曲线。现有的设计放弃了大量的性能和/或存储空间,因为没有沿着这条底部曲线设计。

- 问题来源:通过分析最先进的 LSM 树的设计空间,我们指出了问题的根源,即最坏情况下的更新代价、点查询代价、范围查询代价和空间放大在不同的层次上产生不同的结果。
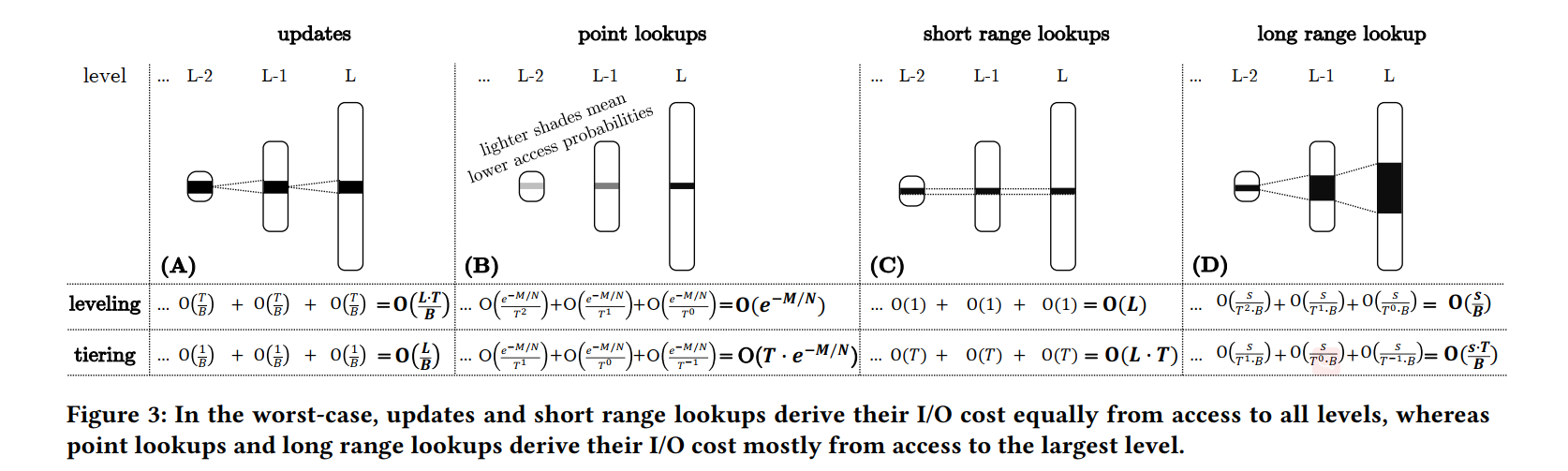
- Update: 更新的 I/O 成本稍后通过更新条目参与的合并操作来分担。虽然较大级别的合并操作需要成倍地增加工作,但它们发生的频率却成倍地减少。因此,更新从所有级别的合并操作中同等地拥有它们的 I/O 成本。
- Point lookups:虽然 图1 中沿顶部曲线的主流设计将跨 LSM-tree 所有级别的 Bloom flters 假阳性率设置为相同,但目前最先进的 Monkey 为更小的层次设置更低的假阳性率。他被证明可以最小化所有过滤器的误报率之和,从而最小化点查找的 I/O。与此同时,这意味着进入较小层此的可能性呈指数级下降,因此大多数点查询 I/O 将直接命中最大的层次(大层次包含更多的数据)。
- Long range lookup:因为 LSM Tree 的容量呈指数级增长,最大层通常包含绝大部分数据,所以该层更可能包含给定键范围内的数据,因此大多数由大范围查询引起的 I/O 都将对最大层进行操作。
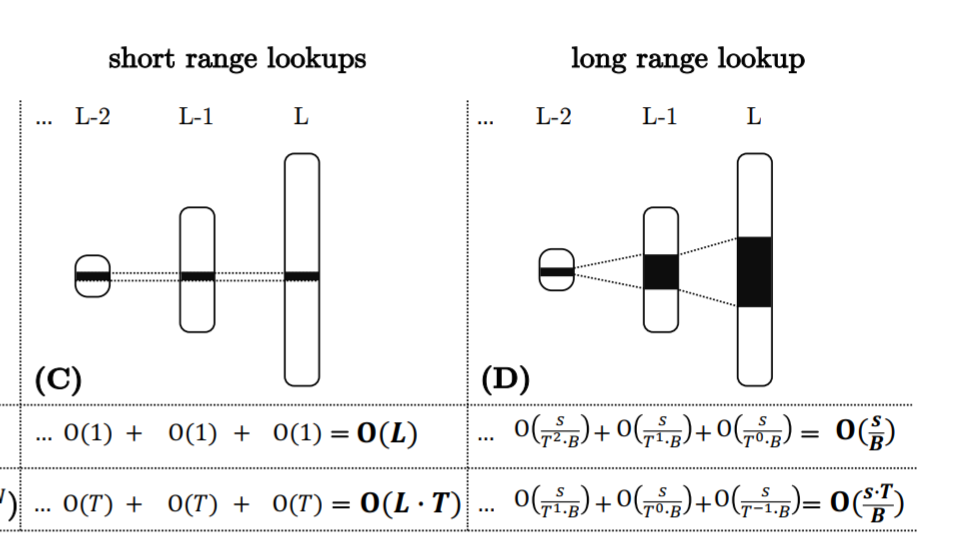
- Short range lookup: 使用极小键范围的范围查找在每次 run 中只能访问大约一个块,而不管 run 的大小,因为每一层 run 的最大个数是固定的,因此小范围查询在所有层次中是相当的。
- Space-Amplifcation:空间放大最差的情况就是较低层次的数据被更新到最大层此,因此在最大层中老旧的数据项比例最大,所以空间放大最为严峻。

- 因为最坏情况下的点查询开销、大范围查询开销、空间放大都主要来源于最大层,LSM-tree 中所有级别的合并操作,除开最大层(即大多数合并操作)在这些指标上几乎没有改进,同时显著增加了更新的平摊成本。这导致了次优的权衡。我们用三个步骤从头开始解决这个问题:
- Solution 1: Lazy Leveling to Remove Superfluous Merging:
- 我们使用 Lazy level 拓展了 LSM-tree 设计思路,这种新设计除去了 LSM-tree 最大级别之外的所有合并。Lazy Leveling 改进了最坏情况下更新的成本复杂性,同时在点查找成本、大范围查找成本和空间放大上保持相同的限制,同时在小范围查找成本上提供具有竞争力的限制。我们证明改进的更新开销可以用来降低点查找开销和空间放大。这生成了 图1 中的底部曲线,它提供了更丰富的时空权衡,这是迄今为止最先进的设计无法实现的。
- Solution 2: Fluid LSM-Tree for Design Space Fluidity.
- 我们引入了 Fluid LSM-tree 作为新一代的 LSM Tree 支持在整个 LSM-tree 设计思路中流畅地切换。Fluid LSM-tree 通过分别控制最大级别和所有其他级别合并操作的频率,相对于 Lazy leveling, Fluid LSM-tree 可以通过在最大级别上合并更少的内容来优化更新,或者通过在所有其他级别上合并更多内容来优化小范围查询。
- Solution 3: Dostoevsky to Navigate the Design Space
- Dostoevsky: Space-Time Optimized Evolvable Scalable Key-Value Store。Dostoevsky 分析找到了Fluid LSM-tree 的调优方法,以最大限度地提高特定应用程序工作负载和硬件在空间放大方面的用户约束,通过精简搜索空间来快速找到最佳调优,并在运行时对其进行物理调整。因为 Dostoevsky 跨越了所有现有的设计,并能够针对给定的应用程序 navigate 到最佳的设计,因此它在性能和空间放大方面严格控制了现有的键值存储。
- Solution 1: Lazy Leveling to Remove Superfluous Merging:
BACKGROUND
- 如下图所示,为了优化写操作,LSM-Tree 初始时缓冲了所有的更新、插入和删除操作到内存中,当 Buffer 满了之后,LSM Tree 将 Buffer 以 Sorted Run 刷回到了第二层存储,LSM Tree 归并排序 runs 是为了:限制查询操作必须访问的 runs 的数量,以及删除老旧的数据项以回收空间。runs 被组织成 L 个呈指数级增长的层次,Level 0 是主存中的 Buffer,其他层次都位于二级存储。
- 在合并的 I/O 开销和查询 I/O 开销以及空间放大之前的权衡可以由两个参数来控制,第一个是相邻两个层次之间的比例 T,T 控制了层级的个数因此决定了一个数据能够在层级之间合并多少次。第二个参数是合并策略,决定了数据项在一个 level 内的合并次数。所有的现有设计都使用了 tiering 或 leveling 两种策略。
- tiering:当一个 level 到达容量时合并该 level 内的 runs
- leveling: 当一个新的 run 出现,就会在 level 中执行合并
- 如下图所示,size ratio 为 4,buffer 大小为一个 entry 的大小。在两种策略中,当 buffer flushing 造成 Level 1 到达容量时触发合并操作。对于 tiering,Level 1 的所有 runs 都被合并成同一个新的 run 放置在 Level 2。而对于 Leveling,合并操作还会包含 Level2 原有的 run。最主要的区别其实是参与 compaction 的 candidate 数据不同。
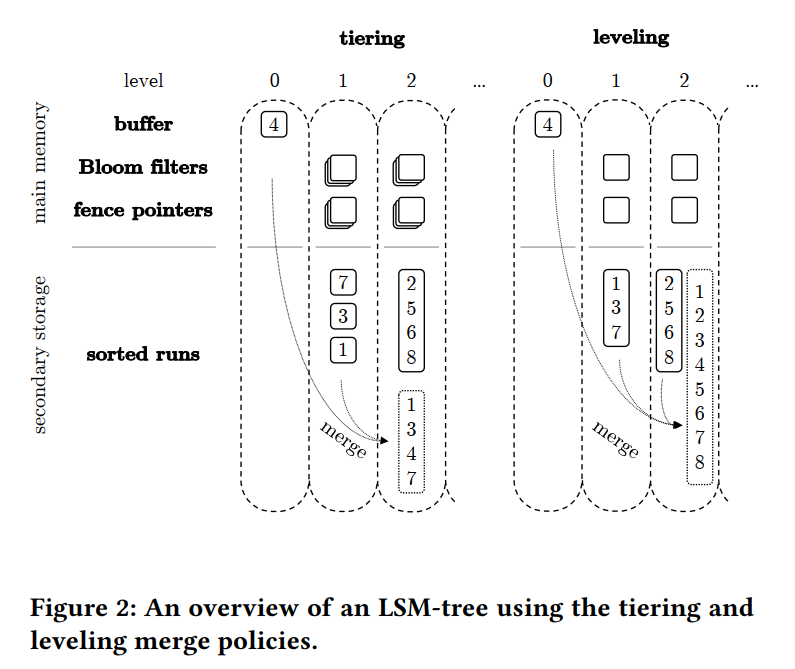
- 本文涉及到的参数的定义。
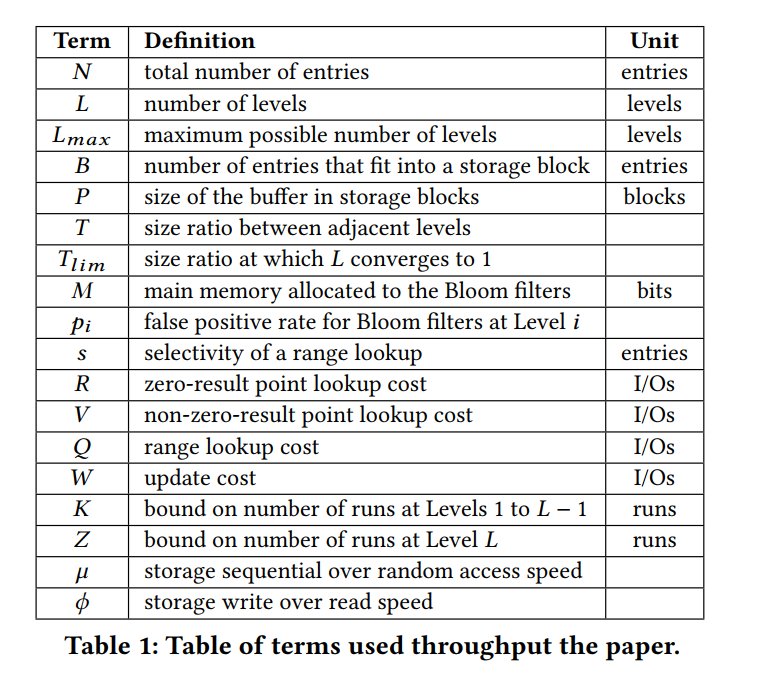
- Number of Levels:Level 0 拥有的数据项个数 B * P。按照 LSM 的布局,放大因子为 T 的话,那么对应 Level i 的数据项个数为 ,总数据项个数为 N 的话,最大层次最多包含 个数据项 。所以层次数 $$L = [log_T(\frac{N}{BP}\frac{T-1}{T})]$$。层级之间的大小比例 T 被限制到 ,其中 被定义成 ,当 size ratio T 达到上界 时,levels 的数量减少到接近 1,超过上界之后将无结构性的变化。大于下界 2 就表明 第 i 级合并操作的结果 run 永远不会大到超过第 i + 1 级。换句话说就是确保了 runs 不会跨多个 levels。因此最高的层级数
- Finding Entries:因为数据项是异地更新,相同 key 的数据的多个版本可能出现在多个 level 中,甚至对于 tiering 策略可能存在于一个 level 的多个 runs 中,为了确保查询操作总是能够找到最新版本的数据,LSM Tree 采用了如下措施:1. 当数据项被插入到 buffer 中且 buffer 中包含相同 key 对应的数据时,新的数据项将代替老的数据;2. 当两个包含相同 key 的数据项的 runs 被合并的时候,只有最新版本的数据将被保留;3. 为了能够获取到来自不同 runs 的相同 key 的不同数据项的插入顺序,一个单独的 run 只能够和相邻时间的 run 进行合并。从而保证当有两个 runs 包含不同版本的相同 key 对应的数据时,younger run 包含的是最新版本的数据。
- Point Lookups:点查询通过从最小到最大层次进行遍历来查询最新版本的数据,对于 tiering 则是在一个 level 中从最新到最老的 runs 中遍历进行查询。当找到一个匹配当前 key 的数据时则终止。
- Range Lookups:范围查询需要查找指定范围的键对应的所有最新的数据,通过对所有 levels 所有 runs 的相关键范围进行排序合并。当 sort-merging 时,识别出来自不同 runs 具有相同 key 的数据,然后丢弃掉老版本的数据。
- Deletes:通过给每个数据项添加一位 flag 来实现。如果查询操作找到了该数据项的最新版本,且该数据项上有该 flag 那么将不会返回对应的 value 给应用。当一个删除的数据项和 最老的 run 合并的时候,该数据将被删除,因为该数据项已经代替了之前所有插入的具有当前 key 的数据。
- Fragmented Merging:为了缓解较大级别上由于长时间合并操作而导致的性能下降,主流设计把 runs 分区成了文件,也叫 Sorted String Tables,然后一次合并一个 SSTable 和下一个 older run 中具有重叠键范围的多个 SSTables,该技术不会影响最坏情况下的合并 I/O 开销,而只会影响这种开销如何调度。在整篇文章中,为了便于阅读,我们将合并操作讨论为具有 runs 的粒度,尽管它们也可以具有 sstables 的粒度。
- Space-Amplifcation:过时条目的存在使存储空间增大的因素称为空间放大。由于磁盘的可承受性,空间放大传统上并不是数据结构设计的主要关注点。然而,SSD 的出现使空间放大成为一个重要的成本问题。我们将空间放大作为成本指标,以提供我们所引入和评估的设计的完整描述。
- Fence Pointers:所有主要的基于 LSM 树的键值存储都在主存中对每个 run 的每个块的第一个键建立索引,也就是图 2 所示的 fence pointer,通常这些指针占据内存空间大小为 O(N/B),但是让查询操作中找到每个 runs 的 key 范围变成了只需要一次 I/O。
- Bloom Filters:为了加速点查找,只需要在主存中为每个 run 维护一个 BloomFilter,点查找在访问存储中相应的 runs 之前首先检查 Bloom flter。如果 filter 返回 true positive,那么查询操作配合 fence pointer 只需要一次 I/O 就能访问对应的 run,从而找到对应的数据项并终止。如果返回 negative,那么将跳过该 run 并节省一次 I/O 操作。但还有 false positive 的情况,浪费一次 I/O 然后再去下一个 run 继续查找该 key。
- Bloom flter 有一个有用的特性,如果它被分割成较小的等大小的 Bloom flter,其中的条目也被等分,每一个新的分区布隆过滤器的 FPR(false positive rate) 渐近与原 filter 的 FPR 相同(虽然实际略高)。为了便于讨论,我们将 Bloom flters 称为非分区的,尽管它们也可以按照工业中的某些设计进行分区(比如每个 run 的每个 block),从而为空间管理提供更大的灵活性。(例如,对于那些不经常被点查询读取的块,可以将其 offload 到存储器中以节省内存)
- Applicability Beyond Key-Value Stores:根据工业上的设计,我们的讨论假设一个键在 run 中与它的值存储在一起。为了便于阅读,本文中的所有图形都将条目描述为键,但它们实际表示键-值对。我们的工作也适用于没有 value 的应用程序(例如,LSM-tree 被用来回答关于键的集合成员查询),其中的值是指向存储在 LSM-tree 之外的数据对象的指针,或者 LSM-tree 被用作解决更复杂算法问题的构建块(例如,图分析), FTL 设计等)。我们将分析的范围限制在基本操作和 LSM-tree 的大小上,以便它可以很容易地应用于这些其他情况。
DESIGN SPACE AND PROBLEM ANALYSIS
- 现在,我们分析更新和查找的最差情况下的空间放大和 I/O 成本是如何从不同的级别派生出与合并策略和大小比例相关的。为了分析更新和查找,我们使用磁盘访问模型来计算每个操作的 I/O 数量,其中 I/O 是从二级存储读取或写入一个块。
- 分析结果如下所示:
- Updates:更新成本通常都是由更新条目参与的后续合并操作产生的,分析假设最坏情况的工作负载,其中所有更新的目标条目都在最大级别。这意味着一个过时的条目不会被删除,直到它相应的更新的条目达到最大级别。因此,每个条目都会在所有级别上合并(即,而不是在某个更小的级别上被最近的条目丢弃,从而减少以后合并操作的开销)。
- tiering:每层合并 O(1) 次,每个合并过程中的 I/O 操作从原始的 run 中拷贝 B 个数据项到新的 run,因此每个数据项平均的更新操作成本开销如图所示。填满 level i,需要 次更新,导致合并操作拷贝 个数据项。
- leveling:到达 level i 的第 j 个 run 触发了一个合并操作,合并操作包括 level i 现有的 runs,这些 runs 是自上次 level i 为空以来到达的前 T−j 个 runs 的合并操作产生的。因此平均每个数据项在该层数据到达容量之前合并了 T/2 次,可以表示为 O(T),同样需要除以一个块对应的 B 个数据项。每 次更新(每次有一个新的 run come in)之后执行一次合并操作,然后拷贝平均 项数据,通过将复制的条目数除以级别 i 的合并操作的频率,我们观察到,在一个比较长的 run 中,每个级别上的合并操作所做的工作量是相同的,直觉是,虽然合并操作在更大的级别上以指数方式完成更多的工作,但它们的频率也以指数方式降低
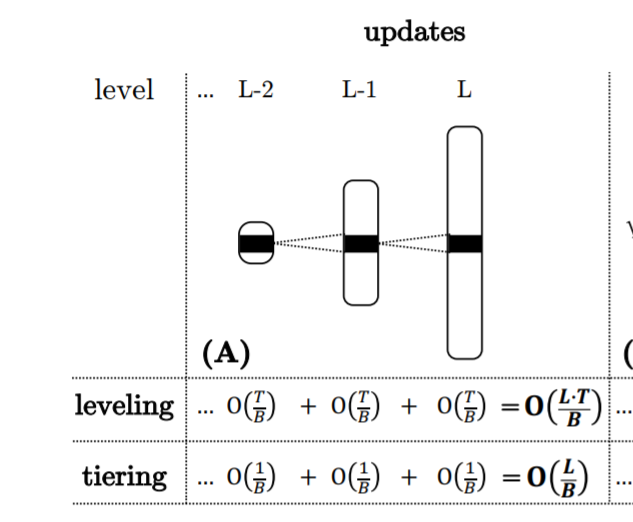
- Analyzing Point Lookups:为了分析最坏情况下的点查找代价,我们将重点放在 zero-result 点查找(例如查询不存在的 Key)上,因为它们最大化了浪费的 I/O 的平均值。这种分析对于插入前判断是否存在的操作就很有用。开销最大的情况即为所有的 BloomFilter 返回 false positive,此时点查询操作会对每一个 run 发起一次 I/O,对于 leveling 浪费的 I/O 为 O(L),对于 tiering 浪费的 I/O 为 O(T · L) 。但实际上,Bloom flters 对于不存在的 key 能节省很大一部分 I/O,在工业中,键值存储对每一个Bloom flters使用 10 位,这会导致误报率(FPR)为每个过滤器约为 1%,出于这个原因,我们将重点放在预期的最坏情况点查找成本上,它将点查找发出的 I/O 数量作为关于 Bloom flters FPRs 的长期平均值进行估计。我们估计这个成本为所有Bloom flters的FPRs之和。原因是,查询单个 run 的 I/O 成本是一个独立的随机变量,其期望值等于相应的 Bloom flter 的 FPR,多个独立随机变量的期望值之和等于它们各自的期望值之和。在工业界的键值存储中,所有级别的 BloomFilter 的每个条目的比特数是相同的。因此,最大级别的 Bloom flter(s) 比所有较小级别的 filter 的总和要大,因为它们以指数形式表示更多的条目。根据公式 ,最大层的 上界被限制在 ,所以对于 leveling,即为 ,对于 tiering,即为 .
- 关于这个问题的最新论文 Monkey 表明,为所有级别的过滤器设置相同的每个条目的比特数并不能最小化浪费的I/O 的预期数量。相反,Monkey 在最大级别上对 filter 中的每个条目重新分配≈1比特,它使用这些比特来设置较小级别上每个条目的比特数,作为不断增加的等差数列:即 Level i 的每个数据项为 ,a 和 b 都是比较小的常数,这导致 FPR 在最大水平上有一个小的、渐近恒定的增加,在较小的水平上有一个指数下降,因为它们包含较少的条目。由于 FPRs 在较小的级别是指数递减的,所以 FPRs 的总和收敛于一个与级别数无关的乘法常数。Monkey 从点查找的复杂性中去掉了一个 L 的因素,这种复杂性导致了 I/O (level)和 I/O (tiering),如图3 (B)所示。对于 zero and non-zero result 的结果点查找以及任何类型的偏差,使用 Monkey 总是有益的。
- 总的来说,我们观察到使用 Monkey 的点查找成本主要来自于最大的 level,因为较小的 level 的 FPRs 呈指数级下降,所以访问它们的可能性也呈指数级下降。
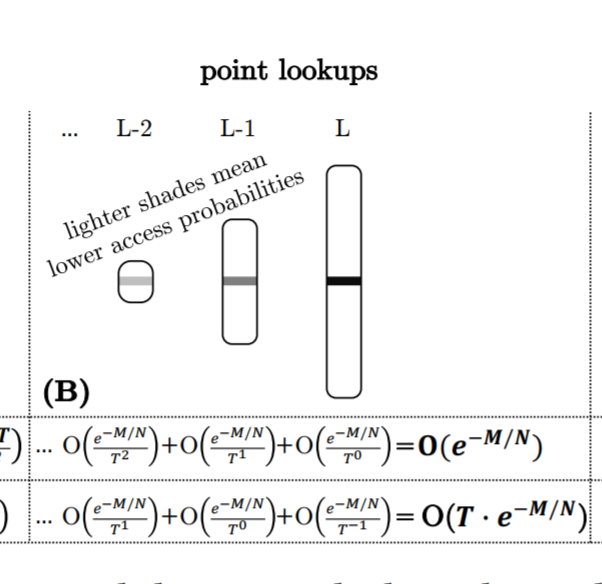
- Analyzing Range Lookups:我们将范围查找的 selectivity 表示为在目标键范围内的所有 run 的唯一条目的数量。范围查找在所有 runs 中扫描和排序合并目标键范围,并从结果集中删除过时的条目。范围查询扫描并排序合并所有 runs 的目标键范围,从结果集中消除老数据。为了分析,如果访问的块数至少是可能的最大级别数的两倍,那么就认为范围查询的范围很大,,在均匀随机分布的更新下,这个条件意味着在目标键范围内的大多数条目都有很高的概率处于最大级别。
- 小范围查询对每个 run 发起近一个 I/O,叠加起来就是 leveling o(L),tiering 就是 O(L·T)。对于长范围查询,在消除过时条目之前的结果集的大小平均是其 selectivity 和空间放大的乘积。我们用这个乘积除以块大小来得到 I/O 成本,tiering 即为 ,leveling 为
- 一个关键的区别是,短范围查找从所有级别获得的开销大致相同,而长范围查找的大部分开销来自访问最大级别
- Updates:更新成本通常都是由更新条目参与的后续合并操作产生的,分析假设最坏情况的工作负载,其中所有更新的目标条目都在最大级别。这意味着一个过时的条目不会被删除,直到它相应的更新的条目达到最大级别。因此,每个条目都会在所有级别上合并(即,而不是在某个更小的级别上被最近的条目丢弃,从而减少以后合并操作的开销)。
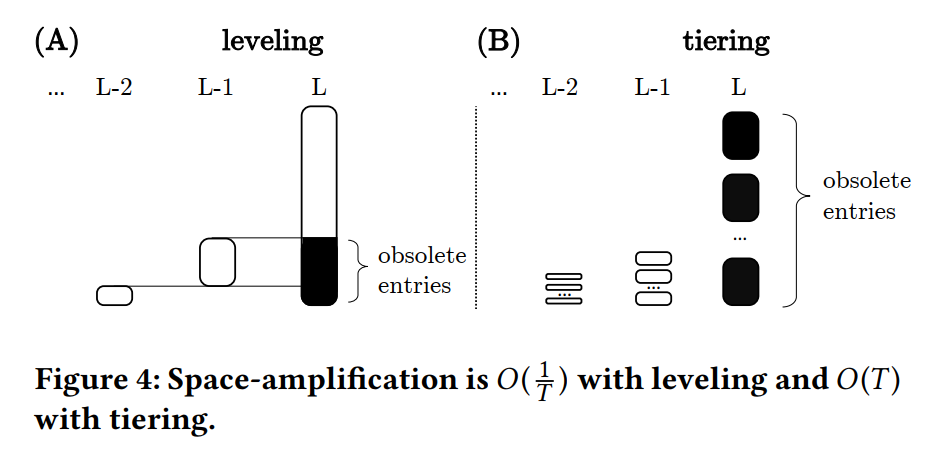
- Analyzing Space-Amplifcation:我们将空间放大定义为条目总数 N 除以唯一条目数 unq,。为了分析最坏情况的空间放大,我们观察到 LSM-tree 的 1 到 L−1 级包含其容量 的一部分,而 L 级包含其容量 的剩余部分。使用 leveing,空间放大最坏的情况是当 Level 1 到 L-1 的条目都是对 Level L 的不同条目的更新时,从而导致 Level L 的最多有 是过时的。空间放大因此是 。对于 tiering,空间放大最坏的情况是当 Level 1 到 L-1 的条目都是对 Level L 的不同条目的更新时,且 Level L 的每个 run 包含相同的数据项集时,Level L 完全由过时的条目组成,所以空间放大是 O(T),因为 Level L 比所有其他 Level 加起来要大 T−1 倍。总的来说,在最坏的情况下,带有 leveling 和 tiering 的空间放大主要是由于在最大级别上存在过时的条目。
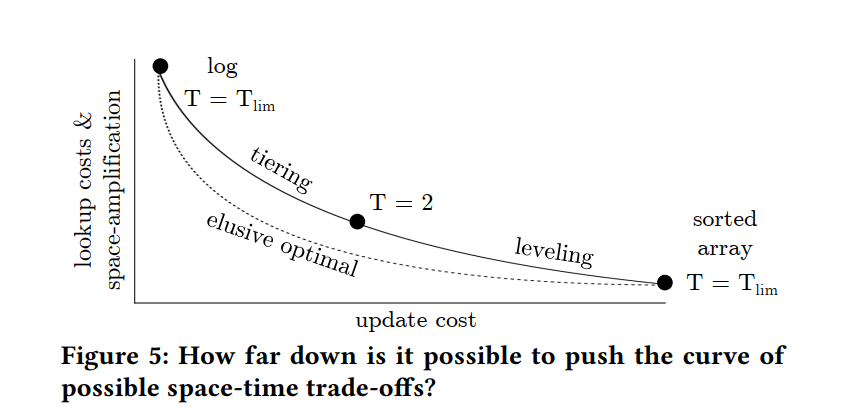
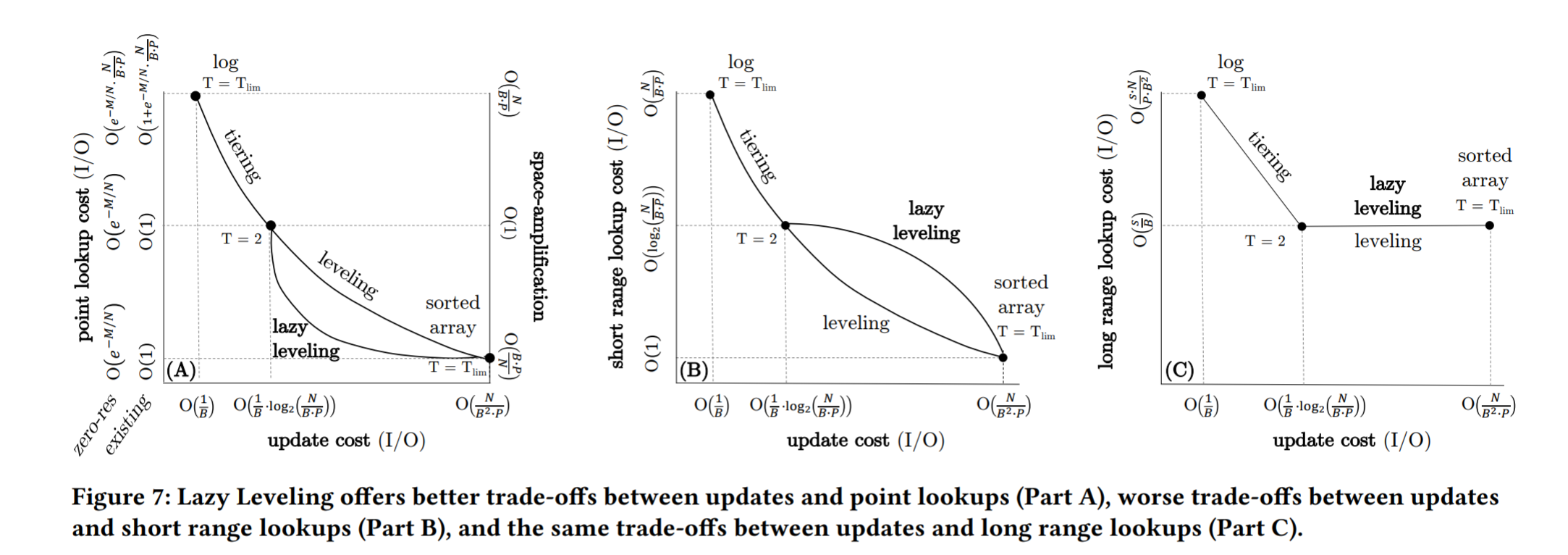
- Mapping the Design Space to the Trade-Off Space:更新成本与查找和空间放大成本之间存在一种内在的权衡。如下图实线绘制了在y轴上查找和空间放大的不同成本,以及在x轴上更新的成本(当我们改变大小比例时)。当大小比例设置为其限制值(意味着存储中只有一个级别)时,tiered 的 LSM-tree 退化为日志,而 leveled 的 LSM-tree 退化为排序的数组。当尺寸比设置为其下限2时,随着 level 和 tiering 的行为趋于一致,性能特征逐渐收敛:级别的数量是相同的,当第二个 run come in 时,每个级别都会触发合并操作。一般来说,随着 leveling/tiering 大小比例的增加,查找成本和空间放大相应 减少/增加,更新成本相应 增加/减少。因此,对权衡空间进行了分区:与分层相比,level 相比于 tiering 具有更好的查找成本和空间放大,更糟糕的更新成本。
- The Holy Grail:图5中的实线反映了Monkey的属性,即当前的最先进的设计。图5 还显示了标记为“难以捉摸的最佳”的虚线。指导我们研究的问题是,其他设计是否可能通过时空权衡更接近甚至达到难以捉摸的最佳设计。
- The Opportunity: Removing Superfluous Merging:我们已经确定了不对称性:点查找成本、长范围查找成本和空间放大主要来自最大的级别,而更新成本来自所有级别。这意味着在更小的级别上合并操作显著地放大了更新成本,同时为空间放大、点查找和远程查找带来的好处相对较小。因此,有一个合并策略的启发,在较小的层次上合并较少次数。
LAZY LEVELING, FLUID LSM-TREE, AND DOSTOEVSKY
Lazy Leveling
-
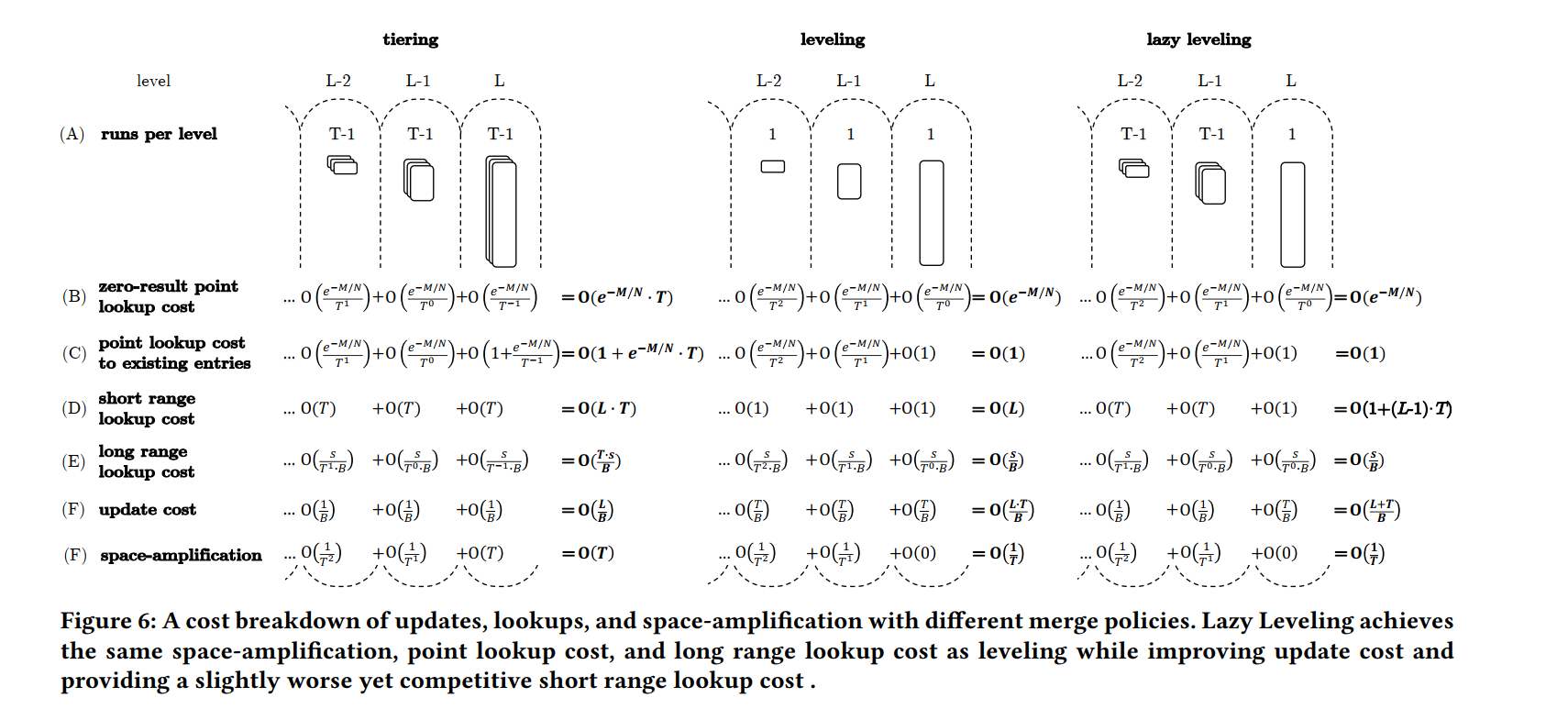
Lazy Leveling 一种合并策略,除了LSM-tree的最大级别之外,它完全消除了合并。其动机是,在这些更小的级别上合并会显著增加更新成本,同时对点查找、大范围查找和空间放大产生的改进相对较小。相比于 Leveling,Lazy Leveling:
- improves the cost complexity of updates
- maintains the same complexity for point lookups, long range lookups, and space-amplifcation
- provides competitive performance for short range lookups.
-
Basic Structure:Lazy Leveling 结构如下所示,其核心类似于缓混合 tiering 和 leveling 两种结构,它在最大 level 上应用 leveling,在所有其他 level 上应用 tiering。结果,最大 level 的 runs 数量为 1,其他 level 的 runs 数量最多为 T−1 (即,合并操作在第 T 个 run 到达时发生)。

-
Bloom Filters Allocation:如何保持点查找的成本复杂性不变,尽管需要在更小的级别上进行更多的查询。我们通过优化不同级别之间的 BloomFilter 内存预算来做到这一点。我们开始建模点查找成本和 filter 的总体内存占用与 FPRs 有关。
-
最坏情况下,每次查找的预期浪费 I/O 数由零结果点查询造成,等于每次运行的 Bloom flters 的假阳性率之和。使用如下等式来建模成本,前面加数的 和 Level L 单个 run 的 FPR 关联,另一个参数则是 Level 1 至 L−1 的 FPRs 的总和。
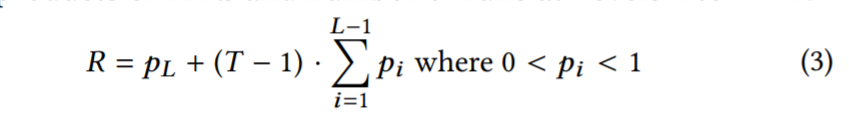
-
然后还建模了内存开销,Level i 的布隆过滤器对应内存开销 和该 Level 的数据条目数 以及 FPR 相关。我们以位元的形式重新排列等式2,并将它应用到每一层。由于任何给定级别上的 filter 都具有相同的 FPR,我们可以直接应用这个方程,而不管级别上 run 的个数。结果是 。总的内存开销 M 如下:
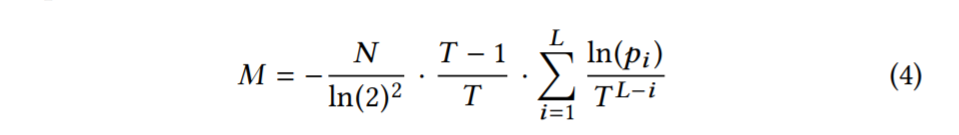
-
我们现在对方程3和方程4彼此进行优化,以找到相对于给定内存预算M,使点查找成本R最小的FPRs。为此,我们使用拉格朗日乘数法。完整的推导在附录 A 中。结果是方程5。
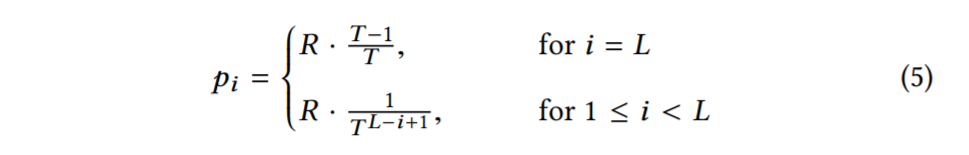
-
Zero-Result Point Lookups:
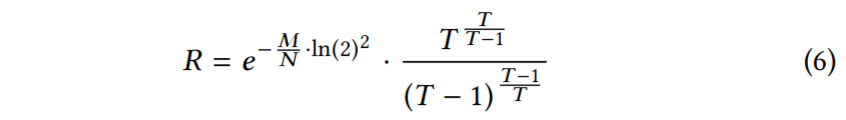
-
Memory Requirement:
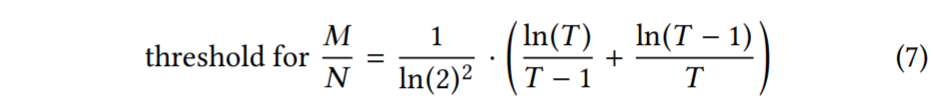
Fluid LSM-Tree
- 为了能够针对不同的工作负载进行所有可能的权衡,我们接下来介绍 Fluid LSM-tree,这是 LSM-tree 的泛化,它支持切换和合并策略。它通过对最大级别和所有其他级别分别控制合并操作的频率来做到这一点。
Basic Structure
- 图8 显示了 Fluid LSM-tree 的基本结构。在最大的级别最多有 Z 个 runs,在每个较小的级别最多有 K 个 runs。为了维持这些界限,每个 Level i 都有一个active run,我们将从 level i-1 中合并进来的 runs。每个 active run 都有一个与其级别容量相关的大小阈值:Level 1 到 L - 1 是 ,Level L 是 ,当 active run 达到阈值时,将在该 level 开启一个新的 active run,最终,当一个级别达到一定容量时,它中的所有运行都会合并并刷新到下一个级别。

Parameterization
- 边界 K 和 Z 用作优化参数,使 Fluid LSM-tree 能够假定不同合并策略的行为。
- K = 1, Z = 1 就是 leveling
- K = T - 1, Z = T - 1 就是 tiering
- K = T - 1, Z = 1 就是 lazy leveling
- Fluid LSM-tree 可以通过增加 Z 在最大层合并地更不频繁来从 lazy leveling 过渡到 tiering, 或者它可以通过减少 K 来在其他层次合并地更频繁从而转变成 leveling。Fluid lsm 树跨越了图7中曲线上和曲线之间所有可能的权衡
开销分析
Dostoevsky
- 我们现在引入 Dostoevsky 来寻找并适应受空间放大约束的 Fluid lsm 树的最佳调谐。Dostoevsky 根据公式 12 中的更新代价W,公式10 中的零结果点查找代价 R,公式 8 中的非零结果点查找代价 V,公式 11 中的范围查找代价 Q 对吞吐量进行建模和优化。它监视这些操作在工作负载中所占的比例,并分别使用系数 w、r、v 和 q 来衡量它们的成本。我们将这个加权代价乘以从存储 Ω 读取一个块的时间,然后取其倒数,得到加权最坏情况吞吐量 τ。
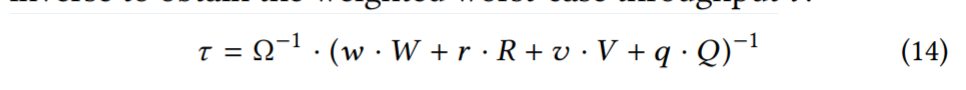
- Dostoevsky 通过迭代参数 T、K 和 Z 的不同值,使等式 14 最大化。它通过两种方法简化了搜索空间。第一个是 LSM-tree 最多有 级,每个级别都有相应的大小比 T,所以只有 个值需要测试。第二个发现是,查找成本 R、Q 和 V 相对于 K 和 Z 单调增加,而更新成本 W 相对于 K 和 Z 单调减少。因此,方程 14 对于 K 和 Z 都是凸的,因此我们可以对它们的值空间进行分治,并在运行时间复杂度为对数的情况下收敛到最优。
- 总体而言, auto-tuning 需要 次遍历,因为每个参数为运行时贡献一个乘法对数因子。为了满足空间放大的给定约束,我们忽略方程 13 高于约束的调谐。由于我们在一个封闭的模型上迭代,执行只需几分之一秒,这使得在运行时找到最佳调优而不影响整个系统性能成为可能。我们在包含 X 个缓冲区刷新(在我们的实现中是 16 个)的时间窗口之间调用自动调优。附录 G 给出了关于适应工作流程和过渡开销的更详细描述。
