- FAST 2019 的文章《SLM-DB Single-Level Key-Value Store with Persistent Memory》
- 这篇论文主要在新型存储器件Persistent Memory上针对传统的 LSM 树进行了优化。
- 本篇论文用于课程论文阅读汇报,故在此总结便于演讲。同时学习 NVM 相关基础知识。
摘要
- 这篇 Paper 主要研究了如何利用新型的字节型寻址器件 PM 来提升 KV 存储系统的性能。提出了一种新型的 KV 存储系统的架构设计 SLM-DB。
- SLM-DB 充分利用 B+ Tree 和 LSM Tree 的优势充分发挥 PM 的特性,实现了较高的读写性能,同时降低了写放大,实现了接近最优的读放大。
Introduction
- 两种传统的 KV 存储类型:一种是基于 B-Tree 的存储引擎,一种是基于 LSM 的存储引擎。
B-Tree
- 特性:在读操作和范围查询操作方面表现较好,在写操作的性能方面表现较差,特别是针对大量的随机小写,并且由于需要动态地维护平衡结构往往就会有很严峻的写放大问题。
- B-Tree 类型的 KV 存储更适用于 读密集型的工作负载。
- 实际的应用产品:KyotoCabinet
LSM Tree
- LSM-Tree 有较高的写性能,通过将相关 KV 缓冲在内存中并批量地将其顺序写入磁盘中。但该结构由于需要维护多层的结构来进行合并压缩归并排序等操作,导致了具有很严重的读写放大问题,在读性能方面表现较差
- LSM Tree 类型的 KV 存储更适用于 写密集型的工作负载。
- 实际的应用产品:BigTable,LevelDB,RocksDB,Cassandra。
Persistent Memory
- 一种新型的存储器件,具有与 DRAM 相当的读写性能,带宽相对 DRAM 较低,但也比 DRAM 拥有更大的容量,最重要的是具有持久性的相关功能
优化方式
读优化
- 利用 PM 的特性维护 B+ Tree 作为索引,加速数据的检索
写优化
- 利用 LSM 的特性来进行 KV 的写入操作,使用 PM 进行缓冲写入,省略了 WAL 的写开销
- 采用单层的 LSM 结构来减小写放大问题带来的影响,但同时需要设计新的压缩算法来保证单层结构中的数据部分有序,从而保证范围查询的性能。
Background & Motivation
LevelDB Introduction
组成部分
- Memory:使用传统的 DRAM 存储和操作 MemTable 和 Immutable Memtable
- Disk:使用磁盘存储和操作多级的 SSTables
核心机制
写流程
- 写流程可以具体划分为插入和更新操作。当有记录要写入时,按照 Key 在 Memtable 中的对应的位置,判断该 Key 是否已经存在,如果存在则进行更新。不存在则相应地写入该 Key 和 Value。
- Memtable 是内存中存数据的地方,这些数据按 Key值排序,为了快速查找,会有红黑树之类的数据结构作为索引。当 Memtable 大小到一定阈值,先状态改变,变成 Immutable Memtable,然后新建一个 Memtable,启动一个后台线程就把 Immutable Memtable 存到一个文件,这个文件就是一个SSTable,相应地将文件刷入磁盘。
- 随着 SSTable File的数量越来越多,触发对应的 Compaction 操作,将对应的 SSTable 文件进行合并,合并到新的数据层上。
读流程
- 首先在memtable中查找,没找到的话,再到 Immutable Memtable 上进行查找,还是没找到的话,再按时间顺序在SSTable文件中查找。当读数据的时候,如果某个记录不存在,需要读取所有的SSTable才能确定。所以一般每个SSTable文件生成的时候会带一个bloom filter,对这一点进行优化。
一致性保证
- 在内存中的写操作采用了 WAL 的机制来进行一致性的保证,统一地先进行日志写的操作,再进行实际的数据插入操作。
- 在磁盘上的数据的一致性保证,采用了 MANIFEST 日志进行保证,针对来自内存的刷会操作和压缩操作都会进行对应的日志记录,主要记录 LSM Tree的结构变化数据。
延申参考链接
Limitation of LevelDB
- LevelDB 的几个核心问题:较低的读性能 和 严峻的读写放大问题
Slow Read Operation
- 最少两次读块的操作:从 LevelDB 中的读流程中我们不难发现,针对在内存中未能命中的数据往往都意味着在磁盘上的每一个 Level 上都会有进行二分查找的操作,首先二分查找定位数据所在的文件 SSTable File;找到对应的文件以后,基于 SSTable File 中存储的数据索引再次进行二分查找,找到对应的数据块。一次读索引块,一次读数据块
- 如果数据块中不包含,则需要进入下一级重复该操作
- 引入 Bloom Filter,一定程度上减小了读操作的开销。
High write and read amplification
Write Amplification
- LSM 通过维护垂直的多级有序数据结构 SSTables 来保证顺序写,从而提高写的速度,但对应的也就引入了维护该结构的开销。
- 需要在不同的层级之间进行归并排序操作,同时需要常常进行数据压缩(Compaction)。
Read Amplification
- 由于 LSM 树的原因,读数据时往往需要在多个层级进行检索
- 读取数据时,往往不仅需要读取该 Key 所对应的数据所在的数据块,还要读取对应的索引块和 Bloom Filter 块,索引块和 Bloom Filter块的数据和可能比 KV 本身大得多。
Persistent Memory
特性
- 非易失,字节寻址
- PM 将通过内存总线进行连接,而不是块接口,所以针对PM的原子写操作应该为8byte大小,相比于传统的存储设备较小。
- 为了保证一致性,需要保证内存操作的顺序
一致性保证
- 为了让内存的带宽最大化,现代的处理器可能会将内存写操作进行指令重排序。所以为了保证内存中的有序写,可能需要显式地使用如 CFLUSH 和 MFENCE等缓存刷新和内存隔离指令。
- 针对一些在 PM 上的写操作,如果数据量超过了 8bytes,在系统故障的情况下可能出现数据部分更新成功的情况,因为 PM 只保证 8bytes 的原子性,为了解决这样的不一致问题,考虑使用日志或者 CoW(Copy on Write)等技术来解决。
基于 LSM 树的优化
提高并行性
- RockesDB(Facebook):利用数据的特性(无重复Key),进行多线程压缩
- HyperLevelDB:通过更为细致的锁管理机制增加了写线程的并行性。
减小写放大
- PebblesDB (SOSP'17):借鉴跳表的思想,弱化全局有序的约束,将每一层进行分段,段之间保证有序,段内无序。
基于硬件的优化(SSD)
- VT-Tree (FAST'13)
- WiscKey (FAST'16):在 LSM-Tree 上做 Key 和 Value 的分离存储
Single-Level Merge DB
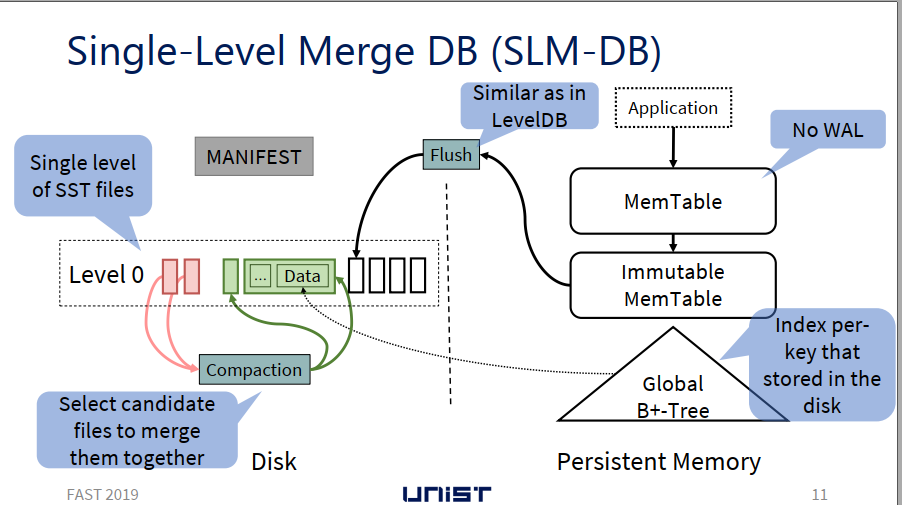
主要贡献
- 使用 PM 存储 MemTable、Immutable MemTable 来提高更强的一致性保证,同时减小一致性的开销
- 在 PM 中引入 B+-Tree 作为索引,提高查询速度
- 将磁盘中的多级数据结构转为单级数据结构,并设计了一种选择性压缩机制
Persistent MemTable

- MemTable 的核心数据结构为 跳表 SkipList
- 跳表的操作,如插入、更新、删除均可用 8bytes 的原子操作完成
- 采用 PM 存储 MemTable,不再需要 WAL 来保证一致性
- 针对跳表的索引部分不需要提供一致性保证,因为可以从原始数据中快速重建
Insert
- Insert(key, value, prevNode)
1: curNode := NewNode(key, value); // Create Node
2: curNode.next := prevNode.next; // Modify currentNode.next pointer
3: mfence(); // 插入内存屏障(读屏障),让高速缓存中的数据失效,重新从主内存加载数据
4: clflush(curNode); // 缓存刷新, 持久化 currentNode 数据
5: mfence(); // 插入内存屏障(写屏障),内存隔离,让写入缓存的最新数据写回到主内存
6: prevNode.next := curNode; // Modify preNode.next pointer
7: mfence(); // 插入内存屏障(读屏障),让高速缓存中的数据失效,重新从主内存加载数据
8: clflush(prevNode.next); // 缓存刷新,持久化 preNode 的修改
9: mfence(); // 插入内存屏障(写屏障),内存隔离,让写入缓存的最新数据写回到主内存
延申链接
B+-Tree Index in PM
When to Build the Tree And Some Key Info
- 当把 KV 键值对从 Immutable MemTable 中往 SSTable 中刷入时,把 Key 相关的索引信息插入到 B+ 树中,作为叶子节点。
- 叶子节点包含的信息有:SSTable File 的标识符,文件内部对应的该 Key 的块的偏移量 和 数据块的大小。
- B+ Tree 的更新操作:更新已有的 KV 对时,首先创建对应该 Key 的索引对象,然后修改原有的在 B+ 树中的指针,指向新的索引对象。旧的索引信息将会被视为垃圾数据进行统一的垃圾回收。
- B+ Tree 的删除操作:当需要删除指定 Key 的数据时,则将该 Key 在 B+ 树中对应的索引信息删除。
- 垃圾回收时使用 PM 管理器如 PMDK 来进行垃圾回收。
Build the Tree
- 当 KV 从 Immutable MemTable 中往 SSTable 刷入时(即 Flush操作),SLD-DB 创建两个后台线程:一个线程用于创建新的 SSTable File,一个用于向 B+ 树中插入索引信息。
File Creation Thread
- 该线程创建一个新的 SSTable 文件,把 Immutable MemTable 中的数据(K-V)写入到该文件中。
- 将该文件执行文件系统相关同步操作,如 fsync,同步到磁盘
- 同步之后,该线程将刚刚存储的 KV 对添加到一个队列中。(由向 B+ 树插入索引的线程创建的队列)
B+ Tree insertion thread
- 创建相应的 KV 索引信息队列
- 待数据写入线程将该队列填入数据之后,依次处理队列中的每个数据,构建 B+ 树
一致性保证
- 待 B+ Tree构建完成以后,将 LSM 树中组织结构的变化(例如 SSTable File 的元数据信息)以追加写的方式写入到 MANIFEST 文件中
其他
- 待完成一致性的日志追加写操作之后,对应的删除PM中的 Immutable Memtable.
Scanning a B+-tree
- SLM-DB 提供了一个迭代器,主要用于扫描存储在磁盘中的 KV 键值对。支持 seek()、value()、next()等操作。
- seek(k):让迭代器指向 key 为 k 的键值对或者当 k 不存在时,指向比 k 稍大的 Key
- next():将迭代器指针移动到下一个 Key
- value():返回该 Key 对应的值
- 在 SLM-DB 中,实现了 B+ Tree 的迭代器,主要用于扫描存储在 SSTables 中的 Key。
Selective Compaction 选择性压缩
Why need Compaction?
- 为了回收部分旧数据。(旧数据是由 Update 操作产生的,更新 Key 对应的值时,之前存储的该 Key 的数据就变成了老数据)
- 提升存储在 SSTables 中的 KV 键值对的顺序性,从而提升 Range Query的性能,以免要查询的 Key 分布散落在多个 SSTable File上
What is Selective Compaction?
- 有选择性地选出一些 SSTables 进行压缩
- SLM-DB 维护一个 候选压缩对象列表。(候选对象为具有一定特性的 SSTables)
When execute?
- 通过启动一个后台的压缩线程来执行:
- 当 SSTable Files的一些结构性数据发生变化时
- 针对一个确定的 SSTable File 出现了多次 seek 操作时
- 当压缩对象候选列表里的文件数量大于一定的阈值时
- 执行时,从候选列表中根据一定的计算规则选出子集进行压缩。该规则主要是计算 SSTable Files 之间的重叠率,通过计算出和候选列表中的其他 SSTable Files 重叠率最高的 SSTable Files,然后进行压缩合并。
How to compact?
- 同上文一样使用两个线程,一个用于文件创建,一个用于索引的插入。
- 合并多个 SSTable Files时,需要检查该文件中的每一个键值对是有效数据还是老旧数据。通过查询 B+树中的索引信息来决定是否有效。如果有效,则需要和其他有效的数据进行归并排序,如果是老旧的数据则对应将其删除。
How to select?
- SLM-DB 实现了三种选择算法:
- Live-Key Ratio Select:有效 Key 比例选择
- Leaf Node Scan:B+树叶子节点扫描选择
- Degree of Sequentially per range query:根据顺序程度进行选择
Live-Key Ratio Select
- SLM-DB 统计每个 SSTable File 的有效 Key 比例,并且设定一个阈值,一旦比例低于该阈值,就会被添加到候选压缩对象列表中。
- Live-Key Ratio 是指每个 SSTable File 中有效 Key 的比例。有效 Key 是指仍然维护在 B+ Tree 中的 Key,也就是仍为该 Key 对应的最新值。
Leaf Node Scan
- 在执行压缩时,将触发一次 B+ Tree 叶子节点的扫描操作,通过循环扫描的方式,统计出存储了 B+ Tree 上有指定 Key 所对应的 SSTable Files 的文件数量,如果文件数量大于阈值,将这些文件添加到候选队列中进行压缩。
- 文件数量意味着在 LSM 结构中存在多个数据文件存储旧值。
Degree of Sequentially per range
- 将 range 操作拆分为多个 子范围查询操作,每个子范围查询对应的 Key 数量相等,然后追踪每个子范围查询访问的 SSTable File 的数量,一旦操作完成,找到访问最多文件的子范围查询,如果对应的文件数大于阈值,把这些对应的文件添加到候选人队列中等待压缩。
- 该方法主要是为了提高数据分布式的顺序性。
存在的问题?
1. B+ 树的引入带来的写放大问题何如?
2. B+ 树索引结构的维护的一致性如何保证?
3. 针对大量小写的情况,B+ 树是否会成为对应的性能瓶颈?
论文延申
Bloom Filter 布隆过滤器
- 本质上布隆过滤器是一种数据结构,比较巧妙的概率型数据结构(probabilistic data structure),特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”。
特点
- 相比于传统的 List、Set、Map 等数据结构,它更高效、占用空间更少,但是缺点是其返回的结果是概率性的,而不是确切的。
- 如果布隆过滤器判断的结果为不存在,那么事实上一定不存在;但如果布隆过滤器判断的结果为存在,那么事实上不一定存在。
原理
- 数据结构:bit 向量/数组(初始化全为0)
- 支持的操作:添加(add)、判断是否存在(ifExsit)
- 不支持的操作:删除(delete)
添加操作
- 使用多个 Hash 函数将要添加的值进行 Hash,得到多个对应的结果,将 bit 向量上的对应位置置为1。
- 每一次新的值都进行相同的操作,将对应位置置为0,但可能置0的位置已经为0了,所以仍然保持为1。
判断操作
- 判断某个值是否已经存在,利用设定好的 Hash 函数对应的求出相应的 Hash 值,看这多个值对应的 bit 向量上是否全为1。如果不全为1,则一定不存在;如果全为1,则可能存在。(原因:不同的值可能产生哈希冲突同时使得某个位置上的值为1)
如何支持删除操作?(是个可以研究的问题)
- 对应的对每一位 bit 进行计数,采用计数删除的方式。但对应的会给每一位增加一个数值的开销。
- 然而要保证安全地删除元素并非如此简单。首先我们必须保证删除的元素的确在布隆过滤器里面。这一点单凭这个过滤器是无法保证的。另外计数器回绕也会造成问题。
如何选择哈希函数个数 k 和布隆过滤器长度 m
- k 次哈希函数某一 bit 位未被置为 1 的概率为:
(1 - \frac {1}{m})^k
- 插入n个元素后依旧为 1 的概率:
1 - (1 - \frac {1}{m})^{kn}
- 标明某个元素是否在集合中所需的 k 个位置都按照如上的方法设置为 1,但是该方法可能会使算法错误的认为某一原本不在集合中的元素却被检测为在该集合中(False Positives)
(1 - (1 - \frac {1}{m})^{kn})^k \approx (1 - e^{-kn/m})^k
- 选择合适的 k 和 m:n 为插入的元素个数,p 为误报率
m = - n\ln p / (\ln 2)^2
k = \frac {m}{n} \ln2
